O assunto deste post é o filtro de Kalman. É uma ferramenta muito útil em sistemas de controle, onde não há certeza nas informações em um sistema.
O que é?
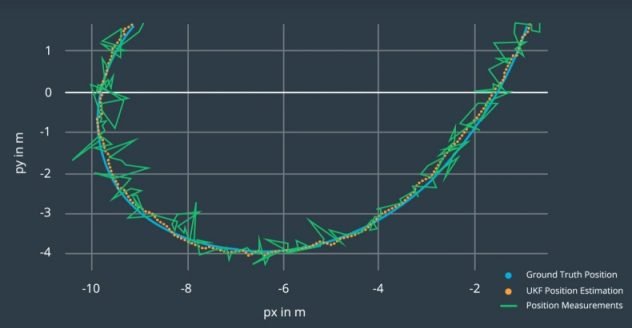
O filtro de Kalman é um algoritmo de otimização para estimar o estado de um sistema com ruído e incertezas. Este filtro recebe medidas imprecisas com ruído, consegue estimar o estado atual com boa precisão e fazer uma previsão do estado futuro.
Por quê usar filtro de Kalman?
Existem situações onde um valor desejado não pode ser medido diretamente, alguns exemplos: A temperatura de motor de avião ou da câmara de combustão de um foguete. Se a temperatura for muito alta, as partes mecânicas serão danificadas. Não é possível medir a temperatura T_{in} diretamente com um sensor, pois este não suporta altas temperaturas. Então o sensor deve ser posicionado em um lugar mais frio e a temperatura deve ser medida indiretamente T_{ext}.
E então, entra o filtro de Kalman, obtendo uma estimativa da temperatura verdadeira T_{in} a partir de T_{ext}. Também pode ser usado para estimar o estado a partir da medida de vários sensores. Por exemplo, um carro ou drone tem GPS, unidade de medida inercial (IMU) e odômetro, este mede a velocidade relativa. Os sensores estão sujeitos a ruído e erros. O filtro de Kalman usa as medições para obter uma estimativa ótima da posição e velocidade do veículo ou drone.
Como funciona?
Nesta parte é explicada uma introdução ao funcionamento do filtro de Kalman padrão (KF), que trabalha somente com equações lineares. Outras variações do filtro serão assunto para futuros posts.
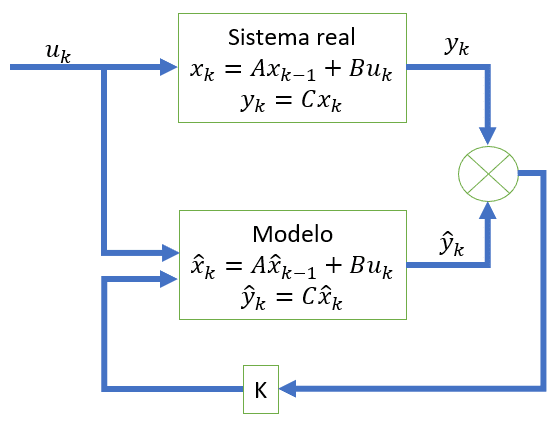
Primeiro é preciso criar um modelo matemático do sistema, porém este é só uma aproximação do sistema real. Supondo que u é a entrada do sistema, y e \widehat{y} são as saídas do sistema real e modelo respectivamente. Enquanto x e \widehat{x} são os vetores de variáveis do sistema real e do modelo respectivamente que têm que estimar.
A parte contornada em vermelho é o observador de estado.
O cálculo do erro e.
e=x-\hat{x}
A, B e C são matrizes. O filtro de Kalman deve ter um contador de tempo discreto k.
Para melhorar a precisão, o ruído do processo w_{k} e a variável aleatória v_{k} devem ser considerados.
v_{k} e w_{k} são curvas gaussianas. Uma curva gaussiana tem a forma mostrada abaixo, neste exemplo, a média \mu é 0 e o desvio padrão \sigma é 1.
v_{k} e w_{k} têm média zero e matrizes de covariância R_{k} e Q_{k} respectivamente.
Algoritmo
O filtro de Kalman tem que combinar os vetores \widehat{x}_{k} e y_{k} para ter a melhor estimativa. O algoritmo tem dois passos: previsão, onde os estados são estimados com as incertezas e atualização, a parte de medição com ruído. Estas são as equações da previsão.
\hat{x}_{k}^{-}=A\hat{x}_{k-1}+Bu_{k}
P_{k}^{-}=AP_{k-1}A^{T}+Q
- \hat{x}_{k}^{-} é o vetor de estimativa a priori, antes da medição.
- P_{k}^{-} é o erro de covariância a priori, a medida da incerteza no estado medido.
- \hat{x}_{k-1} e P_{k-1} são valores que devem ser estimados no início do algoritmo com k=0.
O próximo passo é a parte da atualização e estas são as equações.
K_{k}=\frac{P_{k}^{-}C^{T}}{CP_{k}^{-}C^{T}+R}
\hat{x}_{k}=\hat{x}_{k}^{-}+K_{k}(y_{k}-C\hat{x}_{k}^{-})
P_{k}=(I-K_{k}C)P_{k}^{-}
\hat{x}_{k}^{-} e P_{k}^{-} são usados para calcular o ganho de Kalman K_{k} e atualizar os valores a posteriori de \hat{x}_{k} e P_{k}. O ganho de Kalman indica a influência da medição y_{k} e da estimativa a priori \hat{x}_{k}^{-} para calcular \hat{x}_{k}. Se R tende a zero, o limite do ganho de Kalman é 1, porque na maioria dos casos a matriz C vale 1.
\lim_{R\rightarrow 0}K_{k}=C^{-1}
\hat{x}_{k}=y_{k}
Em contraste, se o erro de covariância P_{k}^{-} tende a zero, o ganho de Kalman também será zero.
\lim_{P_{k}^{-}\rightarrow 0}K_{k}=0
\hat{x}_{k}=\hat{x}_{k}^{-}
Soma-se +1 ao tempo discreto k, a próxima previsão para o instante a seguir é feita e o ciclo continua. Algumas fontes trocam o C por H e colocam z como vetor de medição.
Aplicações na robótica
Robôs autônomos navegando por um ambiente cheio de obstáculos, precisam prever a posição e velocidade futuras para planejar um caminho e chegar na posição certa. Além disso, usam vários sensores mostrando medidas imperfeitas do estado atual.
Este filtro será muito útil em carros sem motorista, o passageiro vai indicar o local para onde quer ir e o carro vai planejar a trajetória considerando a distância e o trânsito.
Também tem aplicação na visão de máquina para saber a trajetória de um objeto.
