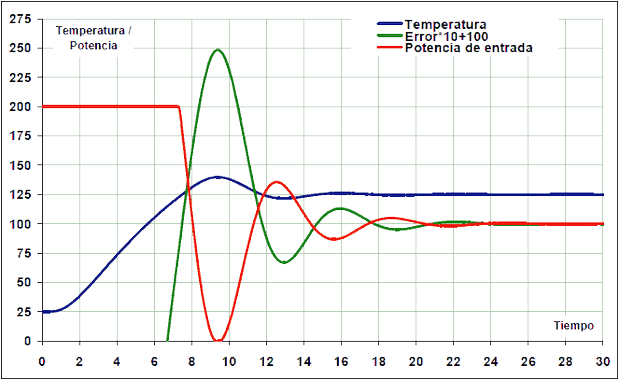
Os métodos clássicos de Ziegler-Nichols, introduzidos em 1942, são alguns dos mais conhecidos e aplicados métodos de sintonia para controladores PID.
Caso não saiba o que é PID, recomendo ler o post sobre o assunto antes de continuar.
Link para post sobre PIDClique aqui
Ziegler-Nichols para resposta ao degrau
Os métodos de Ziegler-Nichols foram desenvolvidos de forma empírica, com observação e prática em muitas plantas diferentes. A planta é considerada uma caixa-preta, não precisa saber suas equações. Mas, deve-se saber a curva de resposta transiente na saída quando ocorre a mudança de set point.

Foi mostrado no post sobre PID, as saídas dos blocos proporcional, integral e derivativo no domínio do tempo. Convertendo para o domínio s, estas saídas ficam como é mostrado a seguir.

A equação e o diagrama do controlador PID em série, no domínio s, respectivamente:
G_{c}(s)=Kp[1+\frac{1}{sT_{i}}]\cdot [1+sT_{d}]=[Kp+\frac{Ki}{s}]\cdot [Kp+sKd]

Equação e diagram do controlador PID paralelo.
G_{c}(s)=Kp[1+\frac{1}{sT_{i}}+sT_{d}]=Kp+\frac{Ki}{s}+sKd

Os ganhos integral Ki e derivativo Kd são:
Ki=\frac{Kp}{Ti}
Kd=Kp\cdot Td
Os métodos de Ziegler-Nichols são um conjunto de equações para calcular os valores do ganho proporcional Kp, tempo integral T_{i} e tempo derivativo T_{d}. Considere a curva de resposta mostrada abaixo.

Este é o conjunto de equações para obter Kp, T_{i} e T_{d}.

Este método pode ser usado em processos de malha aberta, ou seja, sem realimentação. O ajuste dos parâmetros com este método só é aplicável se a resposta do processo ao sinal de degrau for uma curva que lembra um “S”, conforme mostrada acima.
Método do ganho crítico para oscilação
Este é o segundo método de Ziegler-Nichols, deve-se determinar o ganho crítico do sistema para que a saída tenha uma resposta oscilatória estável. Só pode ser aplicado em sistemas de malha fechada, pois a realimentação é um pré-requisito para criar oscilações.
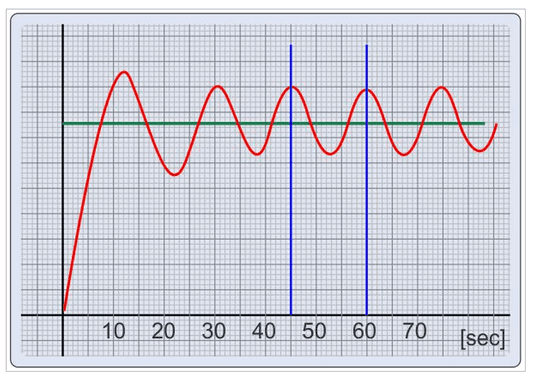
Como achar o valor do ganho crítico K_{CR}? Os blocos I e D devem ser desligados e o ganho proporcional deve ser aumentado até obter a oscilação na saída. Obviamente, isto é feito em simuladores para evitar danos aos processos físicos. Outra alternativa é usar ferramentas computacionais como o rlocus do MATLAB. Após encontrar K_{CR}, deve-se aplicar o conjunto de equações mostrado na tabela abaixo para calcular os parâmetros. P_{CR} é o período crítico da onda de saída.

Com ambos os métodos, pode-se obter um overshoot de no máximo 25% do valor acima do set point. Podem trazer bons resultados de rapidez e estabilidade para a maioria dos sistemas.