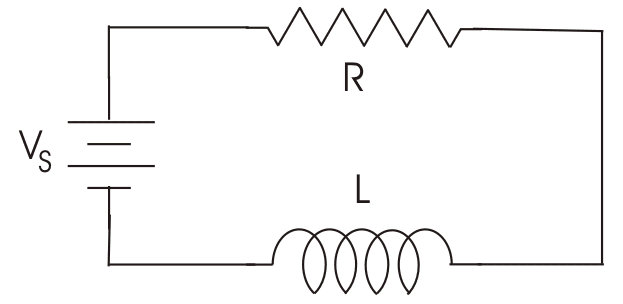
Hoje é mostrado como fazer a análise de circuitos RL que possuem resistores, chaves e indutores.
Fases de carga e descarga nos circuitos RL
Foi construído este circuito abaixo no simulador Qucs para mostrar as fases de carga e descarga. A fonte V1 simula uma fonte DC de onda quadrada com período de 200 μs. Os primeiros 100 μs são a fase de carga e a outra metade do tempo é a fase de descarga.
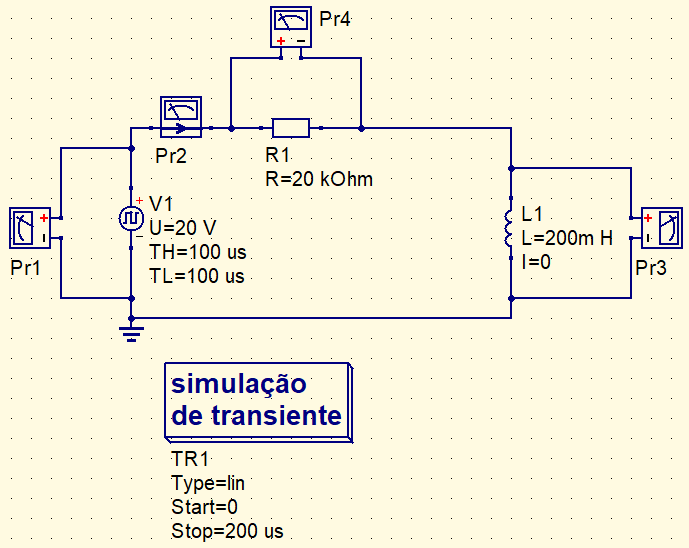
Executando a simulação, temos os seguintes gráficos.




Em circuitos RL, a constante de tempo é calculada dividindo a indutância pela resistência. Neste circuito, o período é 10 μs.
\tau =\frac{L}{R}
Equações da fase de carga
No período transitório de carga, a corrente no indutor segue a equação abaixo.
i(t)=\frac{U}{R1}(1-e^{\frac{-t}{\tau }})
Esta é a equação da tensão no indutor.
v_{L}(t)=U\cdot e^{\frac{-t}{\tau }}
A tensão no resistor.
v_{R}(t)=U\cdot(1-e^{\frac{-t}{\tau }})
No circuito acima, as equações ficam da seguinte forma.
i(t)=1m\cdot(1-e^{\frac{-t}{10\mu }})[A]
v_{L}(t)=20\cdot e^{\frac{-t}{10\mu}}[V]
v_{R}(t)=20\cdot (1-e^{\frac{-t}{10\mu }})[V]
Equações da fase de descarga
As equações da corrente e da tensão no indutor durante a fase de descarga.
i(t)=\frac{U}{R1}\cdot e^{\frac{-t}{\tau}}
v_{L}(t)=V_{L}\cdot e^{\frac{-t}{\tau}}
V_{L} é a soma de todas as tensões dos resistores na mesma malha do indutor e tem polaridade oposta. Vamos usar este circuito como exemplo.
A chave S1 está fechada, enquanto o indutor é carregado. S1 vai abrir em 10 μs e o indutor L1 será descarregado. Esta é a simulação da tensão no indutor, a curva vermelha no gráfico a seguir, mostrando quando S1 é aberta.
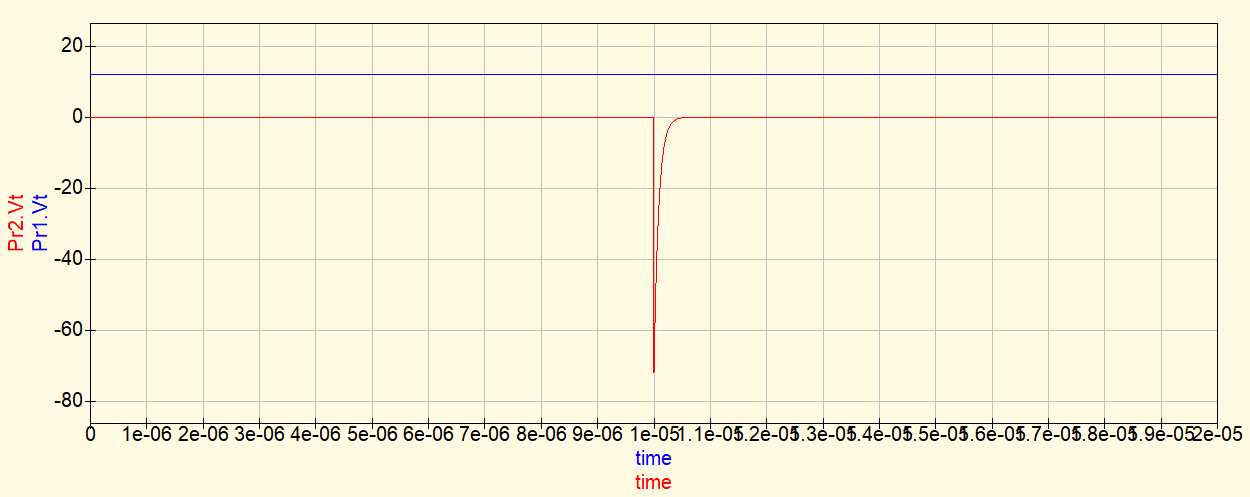
Neste circuito, V_{L} é calculado desta forma.
V_{L}=-(V_{R1}+V_{R2})
V_{R1} e V_{R2} valem 10,38 V e 51,9 V respectivamente. Portanto V_{L} é -62,28 V. A equação da tensão de descarga é:v_{L}(t)=-62,28\cdot e^{\frac{-t}{0,833\mu }}[V]
Valores iniciais
Em alguns problemas os indutores possuem uma corrente inicial I_{i}. Este valor pode ser determinado calculando a corrente que passa pelo indutor e considerando este como um curto circuito, ou é dado pelo problema. A equação é:
i_{L}(t)=I_{f}+(I_{i}-I_{f})e^{\frac{-t}{\tau}}
I_{f} é a corrente do estado estacionário após a transição. Considera-se que os circuitos RL e RC obtenham o estado estacionário depois de 5 constantes de tempo.Aplicação do Teorema de Thévenin
Como analisar circuitos RL mais complexos? É preciso aplicar o Teorema de Thévenin para encontrar a tensão e a resistência equivalentes nos terminais do indutor. O procedimento já foi explicado no post “Teoremas da superposição, Thévenin e Norton”, cujo link está no botão abaixo.
Teorema de ThéveninClique aqui
Aplicando o Teorema de Thévenin, fica muito mais fácil analisar circuitos RL mais complexos.

Calculando a constante de tempo.
\tau =\frac{L}{R_{Th}}
Valores instantâneos
Demonstração da fórmula para calcular o valor instantâneo da corrente em um indutor.
i_{L}=I_{F}+(I_{i}-I_{f})e^{\frac{-t}{\tau}}
i_{L}-I_{F}=(I_{i}-I_{f})e^{\frac{-t}{\tau}}
e^{\frac{-t}{\tau}}=\frac{i_{L}-I_{f}}{I_{i}-I_{f}}
e^{\frac{t}{\tau}}=\frac{I_{i}-I_{f}}{i_{L}-I_{f}}
Aplicando logaritmo neperiano nos dois lados.
ln(e^{\frac{t}{\tau }})=ln(\frac{I_{i}-I_{f}}{i_{L}-I_{f}})
\frac{t}{\tau }=ln(\frac{I_{i}-I_{f}}{i_{L}-I_{f}})
t=\tau ln(\frac{I_{i}-I_{f}}{i_{L}-I_{f}})
Para calcular o valor instantâneo da tensão no indutor.
v_{L}=V_{i}e^{\frac{-t}{\tau }}
t=\tau \cdot ln{\frac{V_{i}}{v_{L}}}
Fórmula da energia armazenada em um indutor
W=\frac{1}{2}LI_{m}
W é a energia armazenada e I_{m} é a corrente no estado permanente após a carga do indutor.