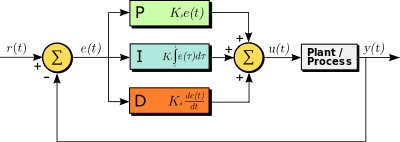
O assunto deste post é a descrição de outros métodos para sintonizar um controlador PID. CHR (Chien, Hrone e Reswick) e CC (Cohen e Coon).
Caso você não saiba o que é PID, acesse o link abaixo antes de continuar.
O método CHR
Todos os métodos de sintonia para o controlador PID consistem em calcular os valores dos ganhos proporcional (K_{p}), derivativo (K_{d}) e integral (K_{i}). O método CHR foi desenvolvido em 1952, como uma alternativa para resolver problemas com resposta ao degrau. Apesar dos ganhos serem menores do que os obtidos por Ziegler-Nichols, o sistema tem mais estabilidade ao adotar o método CHR.

Define regras de ajuste para mudança de setpoint e regulação com robustez a perturbações.
Critérios de desempenho
As tabelas a seguir mostram os cálculos dos ganhos para obter a resposta mais rápida possível com 0 ou 20% de overshoot para ambos os problemas.

Tabela de cálculo dos ganhos para o problema de regulação com robustez
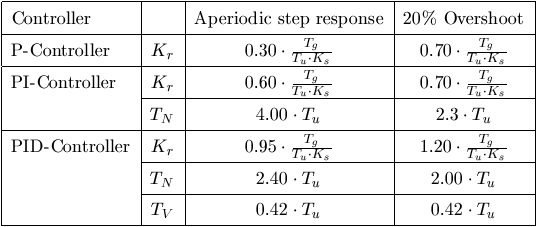
Ki=\frac{Kp}{T_{N}}
Kd=Kp\cdot T_{V}
Tabela de cálculo dos ganhos para o problema servo (mudança de setpoint)

Método Cohen-Coon (CC)
Desenvolvido em 1953, este método também é usado para resposta ao degrau e para um sistema com o tempo morto mais longo, considerando 0,6<\frac{\theta }{\tau }<4,5. No entanto, a robustez ficará ruim se \frac{\theta }{\tau }\leq 2.

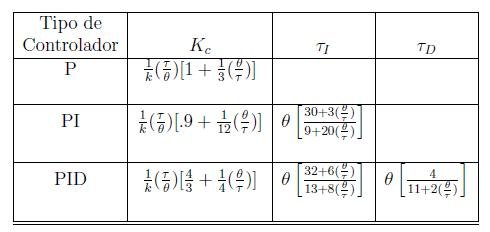
Os métodos Ziegler-Nichols e Cohen-Coon foram criados para obter razão de declínio de 1/4. Caso queira evitar oscilação, o ganho K_{c} deve ser menor do que o calculado.

Além dos apresentados hoje, existem outros métodos de sintonia de PID que ficarão para futuros posts.