Além de série e paralelo, as impedâncias também podem fazer ligações em estrela e triângulo (ou delta). Também são mostradas as transformações.
Ligações estrela e triângulo
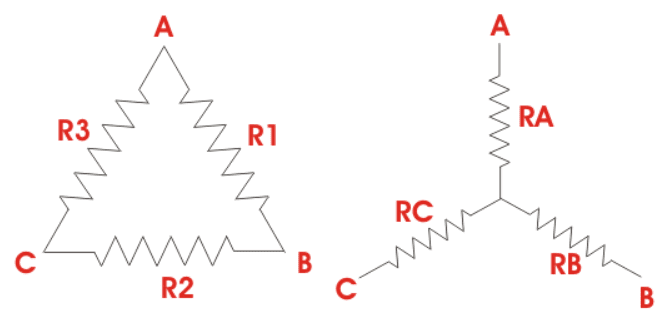
Algumas fontes chamam conexão delta de pi e estrela de T.

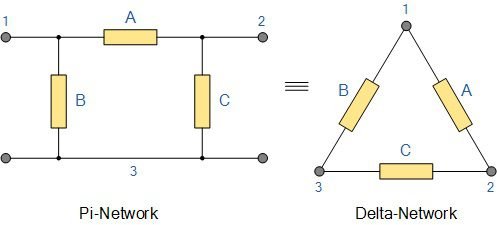
Transformação estrela-triângulo (Y-Δ)
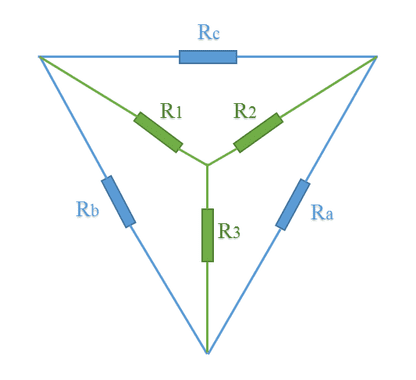
Equações para transformar uma configuração estrela em triângulo.
Ra=\frac{R_{1}R_{2}+R_{1}R_{3}+R_{2}R_{3}}{R_{1}}
Rb=\frac{R_{1}R_{2}+R_{1}R_{3}+R_{2}R_{3}}{R_{2}}
Rc=\frac{R_{1}R_{2}+R_{1}R_{3}+R_{2}R_{3}}{R_{3}}
Transformação triângulo-estrela (Δ-Y)
Equações para a transformação (Δ-Y).
R_{1}=\frac{RbRc}{Ra+Rb+Rc}
R_{2}=\frac{RaRc}{Ra+Rb+Rc}
R_{3}=\frac{RaRb}{Ra+Rb+Rc}
Se todos os resistores forem iguais, as equações ficam muito mais simples. Considerando R_{Y} como o valor do resistor em estrela e R_{\Delta } do resistor em triângulo.
R_{Y}=\frac{R_{\Delta }}{3}
R_{\Delta }=3\cdot R_{Y}
Transformação com capacitores e indutores
E se em vez de resistores, forem capacitores ou indutores?
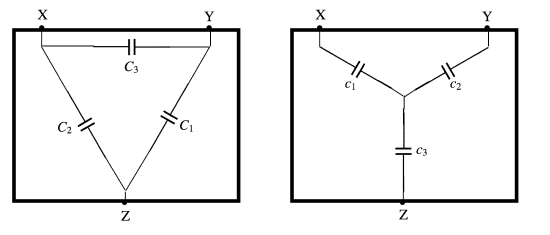
Demonstrando a equação da transformação (Δ-Y) para capacitores.
\frac{1}{c_{1}}=\frac{\frac{1}{C_{2}C_{3}}}{\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}}
c_{1}=\frac{C_{2}C_{3}+C_{3}C_{1}+C_{1}C_{2}}{C_{1}}
c_{2}=\frac{C_{2}C_{3}+C_{3}C_{1}+C_{1}C_{2}}{C_{2}}
c_{3}=\frac{C_{2}C_{3}+C_{3}C_{1}+C_{1}C_{2}}{C_{3}}
As equações da transformação inversa (Y-Δ).
\frac{1}{C_{1}}=\frac{\frac{1}{c_{1}c_{2}}+\frac{1}{c_{1}c_{3}}+\frac{1}{c_{2}c_{3}}}{\frac{1}{c_{1}}}
C_{1}=\frac{c_{2}c_{3}}{c_{1}+c_{2}+c_{3}}
C_{2}=\frac{c_{1}c_{3}}{c_{1}+c_{2}+c_{3}}
C_{3}=\frac{c_{1}c_{2}}{c_{1}+c_{2}+c_{3}}
E quanto aos indutores, os cálculos são semelhantes aos dos resistores.
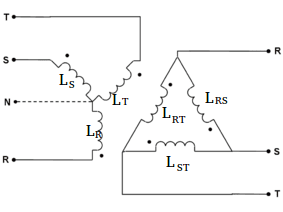
Valores equivalentes de Y para Δ.
L_{RS}=\frac{L_{R}L_{S}+L_{S}L_{T}+L_{R}L_{T}}{L_{T}}
L_{RT}=\frac{L_{R}L_{S}+L_{S}L_{T}+L_{R}L_{T}}{L_{S}}
L_{ST}=\frac{L_{R}L_{S}+L_{S}L_{T}+L_{R}L_{T}}{L_{R}}
Valores equivalentes de Δ para Y.
L_{R}=\frac{L_{RS}L_{RT}}{L_{RS}+L_{RT}+L_{ST}}
L_{S}=\frac{L_{RS}L_{ST}}{L_{RS}+L_{RT}+L_{ST}}
L_{T}=\frac{L_{ST}L_{RT}}{L_{RS}+L_{RT}+L_{ST}}
E para as impedâncias.
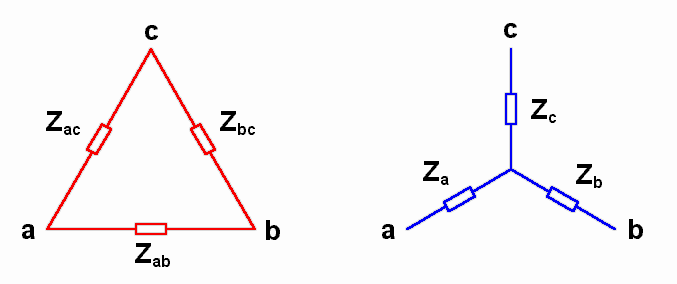
Conversão de Y para Δ.
Z_{ac}=\frac{Z_{a}Z_{c}+Z_{a}Z_{b}+Z_{b}Z_{c}}{Z_{b}}
Z_{ab}=\frac{Z_{a}Z_{c}+Z_{a}Z_{b}+Z_{b}Z_{c}}{Z_{c}}
Z_{bc}=\frac{Z_{a}Z_{c}+Z_{a}Z_{b}+Z_{b}Z_{c}}{Z_{a}}
Conversão de Δ para Y.
Z_{a}=\frac{Z_{ab}Z_{ac}}{Z_{ab}+Z_{ac}+Z_{bc}}
Z_{b}=\frac{Z_{ab}Z_{bc}}{Z_{ab}+Z_{ac}+Z_{bc}}
Z_{c}=\frac{Z_{ac}Z_{bc}}{Z_{ab}+Z_{ac}+Z_{bc}}
3 exemplos de problemas
Vamos encontrar o valor da corrente I neste circuito.
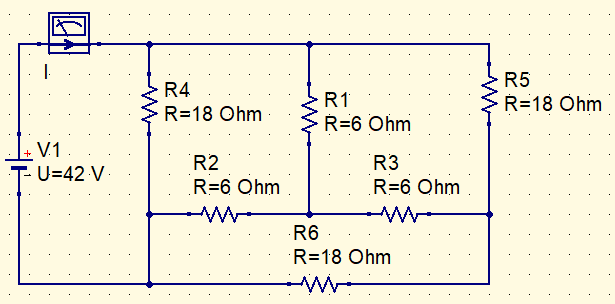
Convertendo a estrela interna em triângulo.
R_{\Delta }=3\cdot R_{Y}
R_{\Delta }=3\cdot 6=18 \Omega
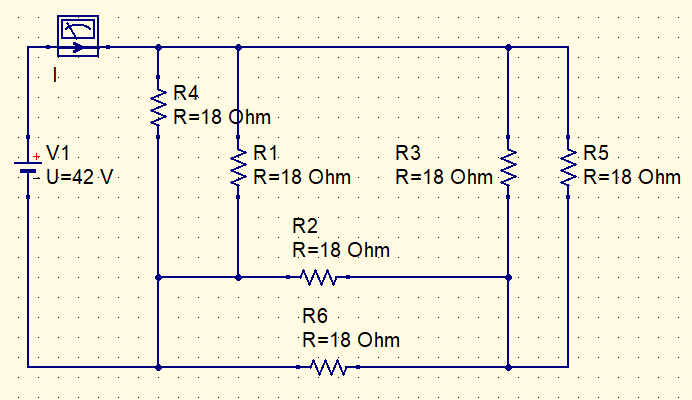
3 pares de resistores ficam em paralelo. Basta simplificar o circuito para achar a corrente I.
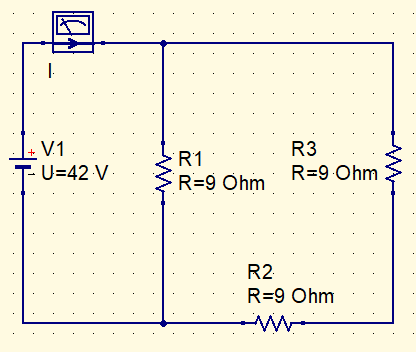
Rt=\frac{9\cdot 18}{9+18}=6\Omega
I=\frac{42}{6}=8A
Como calcular a corrente I neste circuito?
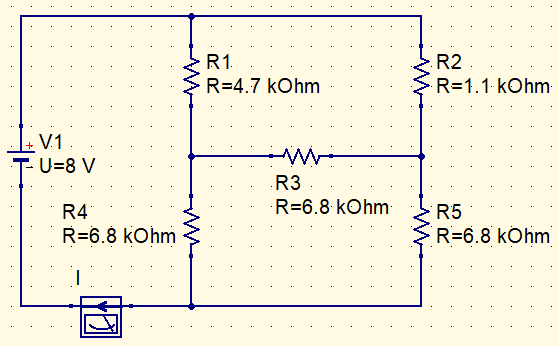
Substituindo os resistores R1, R2 e R3 com a transformação (Δ-Y).
Ra=\frac{4,7k\cdot 1,1k}{4,7k+1,1k+6,8k}=\frac{5,17k}{12,6}=0,41k\Omega
Rb=\frac{4,7k\cdot 6,8k}{4,7k+1,1k+6,8k}=\frac{31,96k}{12,6}=2,53k\Omega
Rc=\frac{1,1k\cdot 6,8k}{4,7k+1,1k+6,8k}=\frac{7,48k}{12,6}=0,59k\Omega
Com o circuito simplificado, fica fácil calcular a corrente.
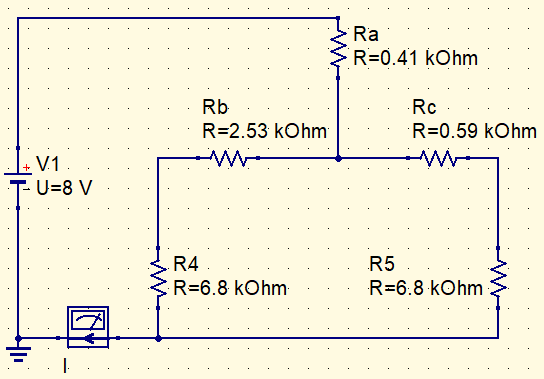
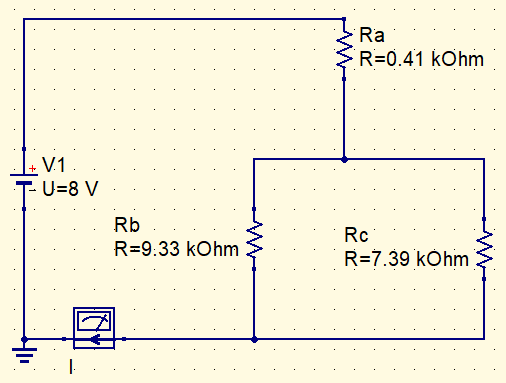
Rt=\frac{9,33k\cdot 7,39k}{16,72k}=4,12k\Omega
I=\frac{8}{0,41k+4,12k}=1,76mA
Como achar a resistência total desta associação de resistores?
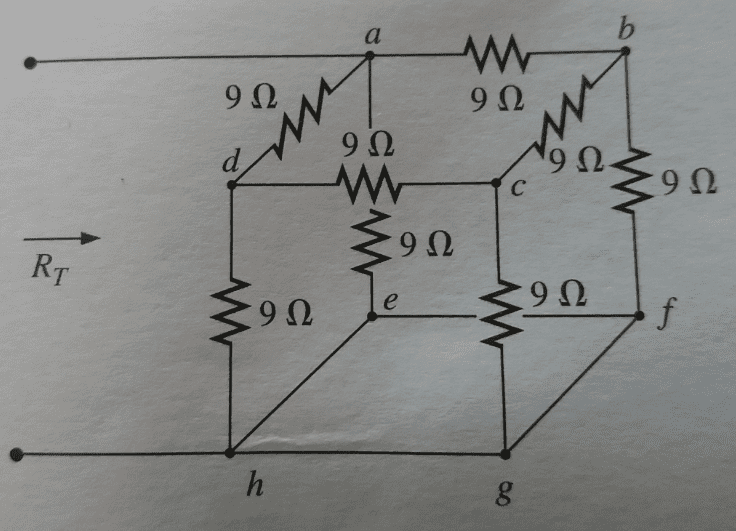
Colocando este cubo em um formato que permita visualizar um grupo de resistores para a conversão.

R_{Y}=\frac{R_{\Delta }}{3}=\frac{9}{3}=3\Omega
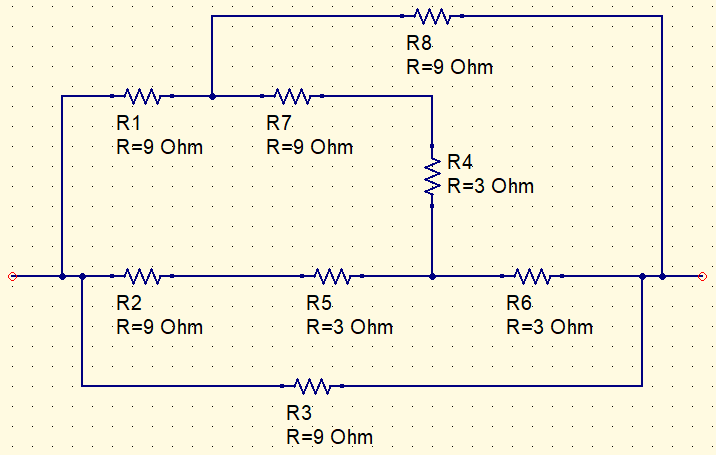

Convertendo o triângulo à esquerda em estrela.
R_{a}=R_{b}=\frac{R1\cdot R2}{R1+R2+R7}=\frac{9\cdot 12}{33}=3,27\Omega
R_{c}=\frac{12\cdot 12}{9+12+12}=4,36\Omega
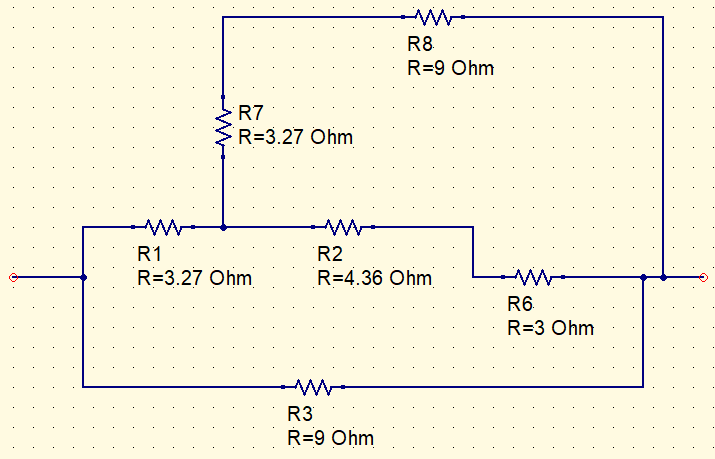
R7+R8=12,27\Omega
R2+R6=7,36\Omega
\frac{12,27\cdot 7,36}{12,27+7,36}=4,6\Omega
3,27+4,6=7,87\Omega
Finalmente, a resistência total Rté:
Rt=\frac{9\cdot 7,87}{9+7,87}=4,19\Omega


