Neste post, são mostrados os conceitos necessários para fazer a análise de circuitos magnéticos, que é muito semelhante a de circuitos elétricos.
Por quê analisar circuitos magnéticos?
O conhecimento da análise deste tipo de circuito é útil para o projeto de componentes que usam campos magnéticos, como por exemplo: relés, transformadores, motores elétricos, geradores, auto-falantes, etc.
Campo magnético e permeabilidade magnética
A densidade do fluxo magnético (B) é definida pelo fluxo magnético (\phi), em Wb (Weber), dividido pela área (A), em m^{2}.
B=\frac{\phi}{A}
A unidade de medida para B é Wb/m^{2} ou T (Tesla). A equação a seguir é a relação entre a densidade de fluxo e a força magnetizante H, esta é em Ae/m (ampère-espira por metro).
B=\mu H
Onde \mu é a permeabilidade magnética. Este é o produto da permeabilidade magnética do vácuo (\mu _{o}), uma constante cujo valor é 4\pi \cdot 10^{-7}H/m, com a permeabilidade relativa (\mu _{r}), que depende do material.
\mu =\mu _{o}\mu _{r}
Analogias com os circuitos elétricos
Relutância
Como é mostrado no post sobre resistência, capacitância, indutância, impedância e reatância, a resistência de um material é calculada usando a fórmula:
R=\rho \frac{L}{A}
Os materiais possuem a relutância (\Re), que é a resistência de um material a um fluxo magnético, cuja equação é:
\Re=\frac{l}{\mu A}
Onde l é o comprimento do material e A é a área da seção transversal. A relutância é medida em rels ou Ae/Wb (ampère-espiras por weber).
Lei de Ohm para circuitos magnéticos
Em um circuito magnético, os geradores de fluxo são indutores, ou bobinas, que produzem a força magnetomotriz (fmm) (\mathfrak{F}), em ampère-espiras, que é a corrente na bobina I multiplicada pelo número de espiras N.
\mathfrak{F}=NI
A equação da Lei de Ohm para circuitos magnéticos.
\mathfrak{F}=\phi \cdot \Re

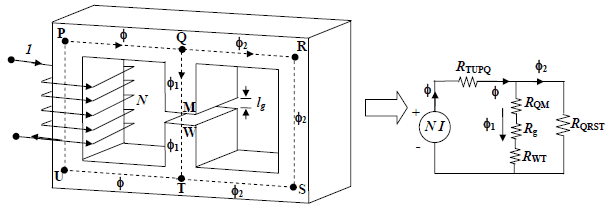
Lei circuital de Ampère para circuitos magnéticos
A Lei de Kirchhoff para tensões diz que a soma das voltagens e quedas de tensão em um circuito de malha fechada é igual a zero. Como foi mostrado no post, cujo link está abaixo.
Análise de circuitos (Parte 1)Clique aqui
A Lei circuital de Ampère afirma que a soma algébrica das elevações e quedas da força magnetomotriz (fmm) em uma malha fechada sempre será igual a zero.
\sum \mathfrak{F}=0
Fluxo magnético
Assim como na Lei de Kirchhoff para as correntes, a soma algébrica dos fluxos que entram em um nó é igual a soma dos fluxos que saem deste mesmo nó.
Entreferro
É o espaço de ar entre os materiais ferromagnéticos, em inglês é chamado de gap. Como a permeabilidade magnética relativa do ar é apenas 1, a força magnetizante H e a queda de fmm são maiores no entreferro do que no núcleo.

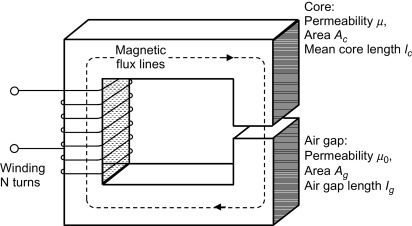
Obtendo a equação para o circuito magnético acima, usando a Lei Circuital de Ampère.
NI=H_{c}\cdot l_{c}+H_{g}\cdot l_{g}
- l_{c} é o comprimento do material ferromagnético por onde passa o fluxo.
- l_{g} é o comprimento do entreferro.
- H_{c} e H_{g} são as forças magnetizantes no núcleo e no entreferro, respectivamente.


