Esta é a primeira parte de uma série de posts que mostram a análise de circuitos práticos que usam o amplificador operacional (amp-op).
Post sobre o funcionamento do amplificador operacional.Clique aqui
Neste post, os amp-ops serão considerados como ideais.
Circuitos com amp-op
Amplificador inversor
Considerando o circuito de amp-op abaixo.
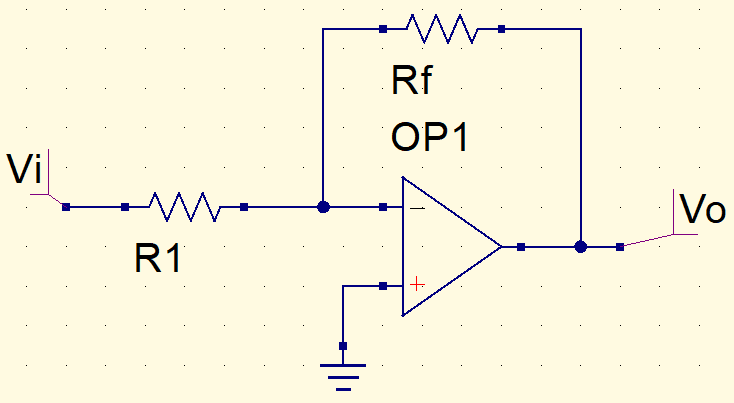
Este é o circuito equivalente.
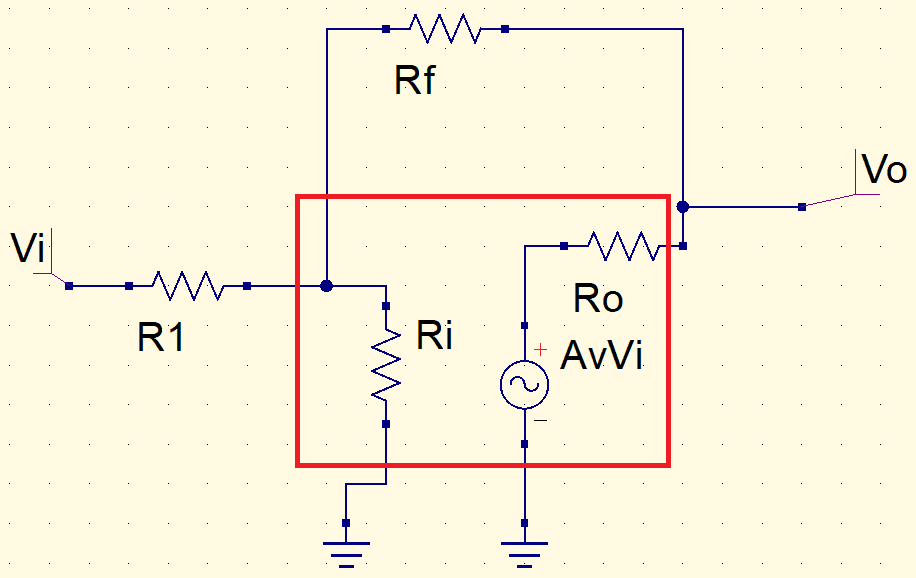
Em um amp-op ideal, a impedância de entrada é infinita e a impedância de saída é zero. Logo, o circuito equivalente fica,
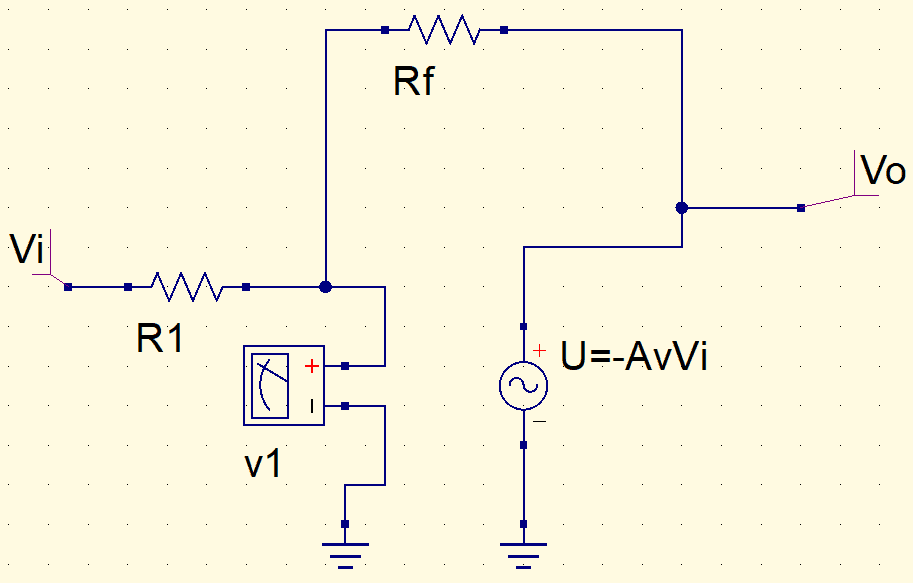
Aplicando o teorema da superposição para encontrar a tensão de v1. Considerando AvVi como zero.
v1_{1}=\frac{Rf}{R1+Rf}\cdot Vi
E Vi como zero.
v1_{2}=\frac{R1}{R1+Rf}\cdot(-AvVi)
v1=v1_{1}+v1_{2}=\frac{Rf}{R1+Rf}\cdot Vi+\frac{R1}{R1+Rf}\cdot(-AvVi)
v1=\frac{RfVi}{Rf+(1+Av)R1}
Geralmente, Av é muito maior que 1 e AvR1 é muito maior que Rf, logo a equação fica,
v1=\frac{RfVi}{AvR1}
A relação entre a tensão de saída e os resistores.
\frac{Vo}{v1}=\frac{-Av\cdot v1}{v1}=-\frac{-AvRfVi}{v1AvR1}
Esta é a equação da tensão de saída do amplificador inversor.
V_{o}=-\frac{R_{f}}{R_{1}}\cdot V_{i}
Amplificador não inversor

Usando a equação de divisão de tensão, chega-se a este resultado:
V_{o}=\left (1+\frac{Rf}{R1}\right )\cdot V_{i}
Buffer de tensão
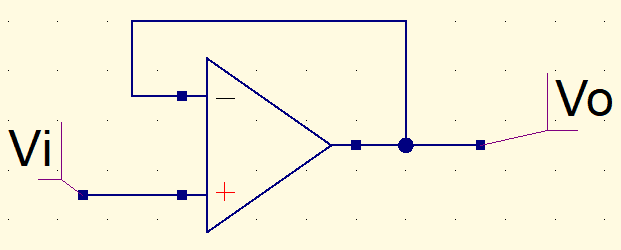
No buffer de tensão ou amplificador de ganho unitário, a tensão de saída é igual à tensão de entrada.
Amplificador somador
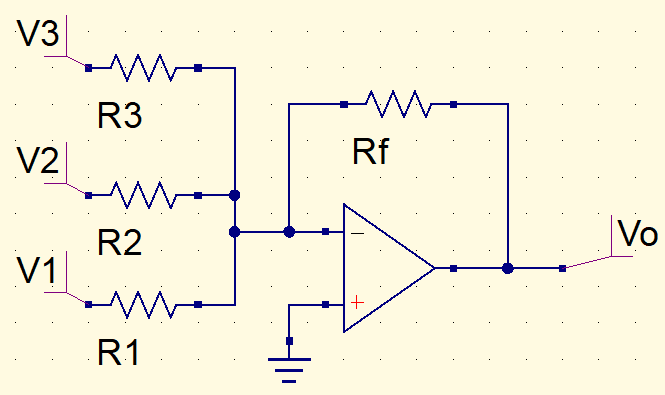
A equação é a soma de vários amplificadores inversores.
V_{o}=-\left(\frac{Rf}{R1}\cdot V1+\frac{Rf}{R2}\cdot V2+\frac{Rf}{R3}\cdot V3\right)
Considere o exemplo de circuito abaixo, que é um amplificador somador com resistores comerciais, vamos calcular a tensão de saída Vo.
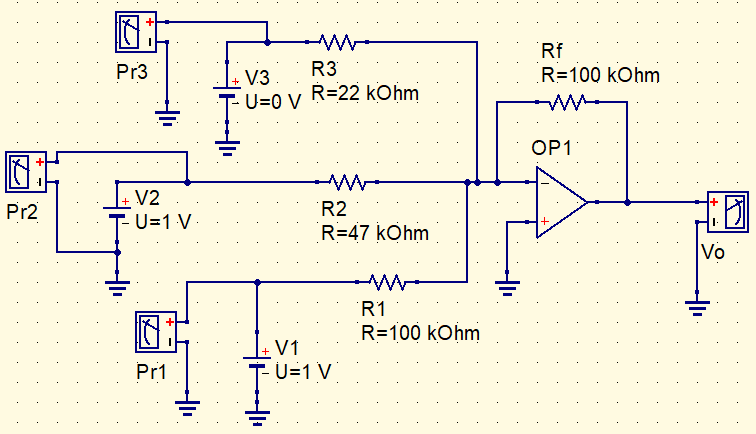
Aplicando a equação.
Vo=-\left(\frac{100k}{22k}\cdot 0+\frac{100k}{47k}\cdot 1+\frac{100k}{100k}\cdot 1\right)
Vo=-\left(2,12\cdot 1+1\cdot 1\right)=-3,13V
O resultado da simulação do circuito.

Agora, vamos fazer um ajuste nas tensões de entrada.

Aplicando novamente a mesma equação.
Vo=-\left(4,54\cdot 1+0+1\cdot 1\right)=-5,54V
E fazendo a simulação.

O que este exemplo mostra é que o somador pode ser usado como um conversor digital-analógico. A entrada com o resistor R3 é o bit mais significativo (MSB) e a entrada com R1 é o bit menos significativo (LSB). Na primeira simulação, as entradas eram ‘011’, que gerou próximo de 3V, sendo que ‘011’ é 3 em binário. Enquanto na segunda simulação, as entradas eram ‘101’, que é 5 em binário, e a saída foi próxima de cinco.
Integrador

No inversor, se o resistor de realimentação for substituído por um capacitor, o circuito se torna um integrador. Considerando o terra virtual,
I=\frac{Vi}{R}=-\frac{Vo}{X_{C}}
X_{C} é a reatância capacitiva.X_{C}=\frac{1}{j\omega C}=\frac{1}{sC}
Na notação de Laplace, j\omega=s.
\frac{Vi}{R}=-\frac{Vo}{\frac{1}{sC}}=-sCVo
\frac{Vo}{Vi}=\frac{-1}{sCR}
Colocando a equação no domínio do tempo.
v_{o}(t)=-\frac{1}{RC}\int v_{i}(t)dt
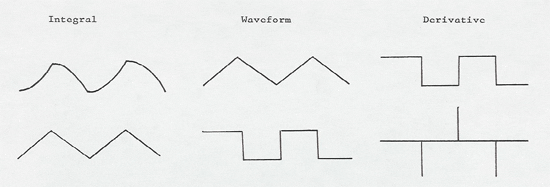
Se a entrada for uma onda senoidal, a saída será uma senoide atrasada a 90º em relação à entrada.
Derivador
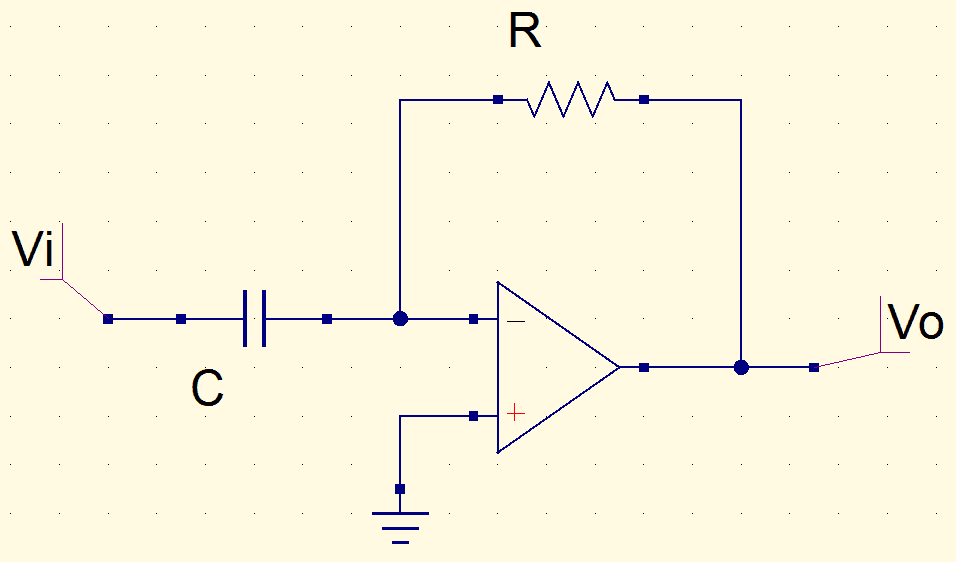
Trocando as posições do resistor e do capacitor, temos o derivador, que é o oposto do integrador. Portanto, o sinal de saída é a derivada do sinal de entrada. Neste circuito, se a entrada for uma senoide, a saída também será uma senoide, porém 90º adiantada em relação à entrada. Abaixo é a equação da tensão de saída no domínio do tempo.
v_{o}(t)=-RC\frac{dv_{i}(t)}{dt}


