Neste post é mostrado como analisar circuitos RC, ou seja, com resistores e capacitores.
Fase de carga
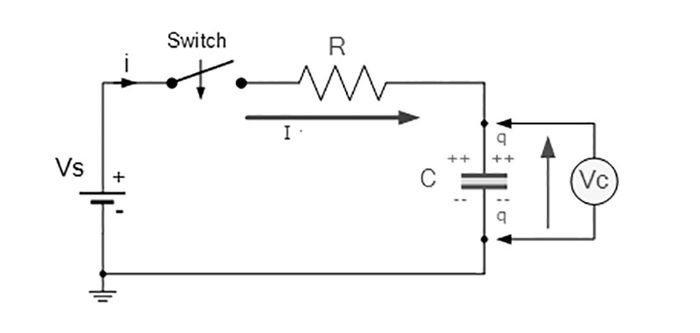
Vamos considerar o circuito abaixo. Neste simulador, eu usei um gerador de pulso com um período longo para simular uma fonte DC com uma chave que fecha no instante t=0.

O capacitor não permite a variação abrupta de tensão, existe um período transitório de carga do capacitor. Durante a fase de carga, a tensão no capacitor obedece a esta curva em azul no gráfico a seguir. O sinal da fonte é em vermelho.

E este é o gráfico da corrente.

A tensão no capacitor segue esta equação.
V_{C}(t)=V1(1-e^{\frac{-t}{\tau}})
- V_{C}(t) é a tensão no capacitor em função do tempo.
- V1 é a tensão da fonte DC.
- \tau é a constante de tempo calculada desta forma.
\tau=RC
A corrente no capacitor I_{C}(t) segue esta equação.
I_{C}(t)=\frac{V1}{R}e^{\frac{-t}{\tau}}
Fase de descarga
A fonte de pulso deste circuito foi ajustada para começar com 6 V e mudar para 0 V. Simulando uma chave abrindo em t=0.

O gráfico da tensão de descarga no capacitor em vermelho.

A corrente de descarga no capacitor e a fórmula respectivamente.

I_{C}=-\frac{V1}{R}e^{\frac{-t}{\tau }}
Valores iniciais
Em algumas situações de análise de circuitos RC, o capacitor já possui uma carga. Neste caso, deve usar esta equação abaixo. V_{i} é a tensão inicial antes da carga e V_{f} é a tensão final após a carga.
V_{C}(t)=V_{f}+(V_{i}-V_{f})e^{\frac{-t}{\tau}}
Se V_{i} for igual a zero, fica igual a equação de carga do capacitor.
V_{C}(t)=V_{f}+(0-V_{f})e^{\frac{-t}{\tau}}
V_{C}(t)=V_{f}(1-e^{\frac{-t}{\tau}})
Curva da tensão no gráfico, aqui o capacitor tem alguma tensão inicial. Neste caso começa em 2 V.

O gráfico da corrente é o mesmo do caso sem carga inicial no capacitor. Para calcular a corrente de pico I_{p}.
I_{p}=\frac{V1-V_{C}}{R}
Valores instantâneos
Como determinar a tensão ou a corrente de um capacitor em um determinado instante de tempo? Fazendo a demonstração para obter a fórmula.
V_{C}=V_{f}+(V_{i}-V_{f})e^{\frac{-t}{\tau}}
V_{C}-V_{f}=(V_{i}-V_{f})e^{\frac{-t}{\tau}}
\frac{1}{e^{\frac{-t}{\tau}}}=\frac{V_{i}-V_{f}}{V_{C}-V_{f}}
e^\frac{t}{\tau}=\frac{V_{i}-V_{f}}{V_{C}-V_{f}}
Aplicando logaritmo neperiano nos dois lados.
ln(e^{\frac{t}{\tau}})=ln(\frac{V_{i}-V_{f}}{V_{C}-V_{f}})
\frac{t}{\tau}=ln(\frac{V_{i}-V{f}}{V_{C}-V_{f}})
Esta é a equação para calcular o instante de tempo em um valor V_{C}.
t=\tau ln(\frac{V_{i}-V{f}}{V_{C}-V_{f}})