Teorema da máxima transferência de potência
Existem situações, onde é necessário saber qual é o valor da resistência ou impedância necessária em uma parte do circuito para transferir a maior quantidade de potência possível para aquela carga. Esta é uma aplicação do teorema de Thévenin, já foi mostrado em um post.
Superposição, Thévenin e NortonClique aqui
O circuito abaixo é usado como exemplo. Tem que calcular o valor de RL para que a máxima potência seja transferida a este resistor.
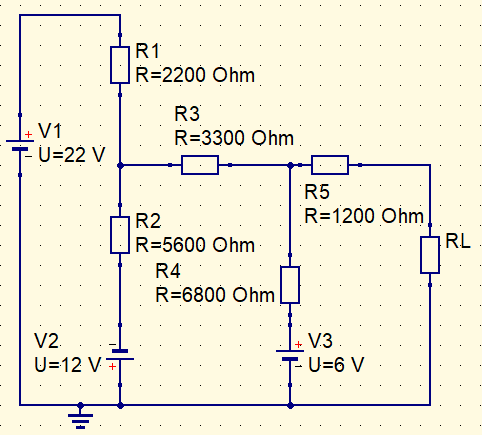
Primeiro temos que encontrar a resistência e a tensão de Thévenin. O método já foi explicado no post sobre o assunto, cujo link está acima. Neste exemplo, a resistência de Thévenin Rth e a tensão Vth são respectivamente.
Rth=4,04k\Omega
Vth=9,77 V
Para ter máxima transferência de potência, RL deve ser igual a resistência equivalente de Thévenin do circuito.

Calculando a potência transferida para RL.
P_{L}=I_{L}^{2}\cdot R_{L}=(\frac{V_{Th}}{2R_{Th}})^{2}\cdot R_{Th}=\frac{V_{Th}^{2}}{4R_{Th}}
O valor da potência.
P_{L}=5,906mW
Teorema de Millman
Os 2 teoremas de circuito a seguir são pouco conhecidos. O teorema de MIllman determina que várias fontes de tensão em paralelo são equivalentes a uma única fonte.

Como converter várias fontes em uma? Primeiro, todas as fontes de tensão devem ser convertidas em fontes de corrente. Já foi demostrado como fazer isso no post “Análise de circuitos (Parte 1)“.

Nesta conversão, as resistências se tornam condutâncias G. Estas são o inverso da resistência, cujo valor é em Siemens (S).
G=\frac{1}{R}
O próximo passo é converter todas as fontes em uma única fonte de corrente.
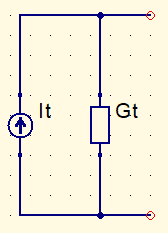
It=I_{1}+I_{2}+I_{3}
Gt=G_{1}+G_{2}+G_{3}
Finalmente, converta a fonte equivalente de corrente It em uma fonte de tensão. A condutância volta a ser resistência.
 R_{eq}=\frac{1}{Gt}=\frac{1}{G_{1}+G_{2}+G_{3}+...+G_{N}}
R_{eq}=\frac{1}{Gt}=\frac{1}{G_{1}+G_{2}+G_{3}+...+G_{N}}
V_{eq}=\frac{It}{Gt}=\frac{\pm V_{1}G_{1}\pm V_{2}G_{2}\pm V_{3}G_{3}\pm ...\pm V_{N}G_{N}}{G_{1}+G_{2}+G_{3}+...G_{N}}
R_{eq}=\frac{1}{\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+...+\frac{1}{R_{N}}}
Este teorema também pode ser utilizado para encontrar a máxima transferência de potência para uma carga.
Teorema da substituição
Segundo o livro Análise de Circuitos, do Robert L. Boylestad, 12ª edição, este teorema afirma:
Se a corrente que atravessa um ramo qualquer de um circuito bilateral de corrente contínua e a tensão entre os terminais do mesmo ramo são conhecidas, esse ramo pode ser substituído por qualquer combinação de componentes que mantenha inalteradas a tensão e a corrente associadas ao ramo escolhido.
Este teorema é uma forma de simplificar circuitos elétricos, substituindo uma parte do circuito por uma fonte de tensão ou corrente. Pode ser usado junto com outros teoremas de circuito.




