Esta é a terceira e última parte da série de posts sobre polarização de um transistor BJT. Outras configurações de circuito são mostradas.
As outras partes podem ser acessadas clicando nos botões a seguir.
Como polarizar o transistor BJT? (Parte 1)Clique aqui
Como polarizar o transistor BJT? (Parte 2)Clique aqui
Polarização do transistor BJT por divisor de tensão
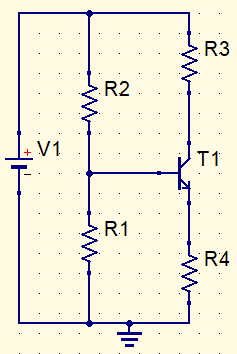
Esta configuração é mais estável que a polarização do emissor. Ou seja, as variações da corrente de coletor (I_{C}) e tensão coletor-emissor (V_{CE}) são muito pequenas quando muda o β. Existem dois métodos conhecidos de análise deste circuito.
Análise exata
Usando este circuito como exemplo para aplicar a análise exata, calculando os valores de I_{C}, V_{CE}, I_{B}, V_{E} e V_{B}.
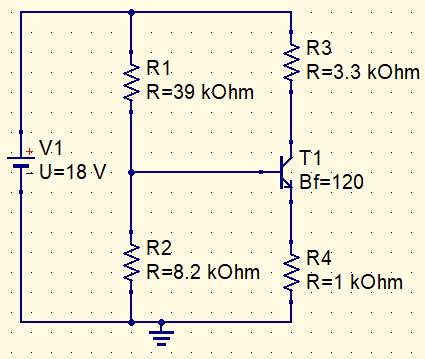
É necessário o circuito equivalente de Thévenin da área dentro do quadrilátero vermelho, cuja saída, onde ficam os terminais, é apontada pela seta.
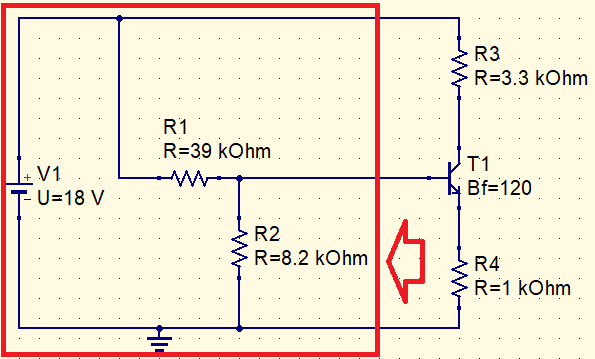
Calculando a resistência e a tensão de Thévenin respectivamente.
R_{th}=R1||R2=\frac{R1\cdot R2}{R1+R2}=\frac{39k\cdot 8,2k}{39k+8,2k}=6,775k\Omega
E_{th}=\frac{R2\cdot V1}{R1+R2}=3,12V
Aplicando a equação abaixo para calcular a corrente de base I_{B}.
I_{B}=\frac{E_{th}-V_{BE}}{R_{th}+(\beta +1)\cdot R_{E}}
I_{B}=\frac{3,12-0,7}{6,78k+(120 +1)\cdot 1k}=18,93\mu A\simeq 19\mu A
I_{C}=\beta \cdot I_{B}=120\cdot 19\mu =2,28mA
Calculando a tensão coletor-emissor V_{CE}.
V_{CE}=V_{CC}-I_{C}\cdot (R_{C}+R_{E})=18-2,28m\cdot (3,3k+1k)=
Encontrando os demais valores.
I_{E}=I_{B}+I_{C}=2,299mA\simeq 2,3mA
V_{E}=I_{E}\cdot R_{E}=2,3m\cdot 1k=2,3V
V_{BE}=V_{B}-V_{E}\rightarrow 0,7=V_{B}-2,3\rightarrow V_{B}=3V
Análise aproximada
Para saber se pode aplicar a análise aproximada em um circuito, deve-se fazer o seguinte teste. Se a condição abaixo for verdadeira, pode aplicar esta análise.
\beta \cdot R_{E}\geq 10\cdot R_{2}
120 \cdot 1k\geq 10\cdot 8,2k
120k\geq 82k
Como a condição acima é verdadeira.
V_{B}=\frac{R_{2}\cdot V_{CC}}{R_{1}+R_{2}}
V_{B}=\frac{8,2k\cdot 18}{39k+8,2k}=\frac{147,6}{47,2}=3,12V
V_{BE}=V_{B}-V_{E}\rightarrow V_{E}=3,12-0,7=2,42V
I_{E}=\frac{V_{E}}{R_{E}}=\frac{2,42}{1k}=2,42mA
Nesta análise, pode-se considerar I_{E}\cong I_{C}. Calculando V_{CE}.
V_{CE}=V_{CC}-I_{C}\cdot (R_{C}+R_{E})
V_{CE}=18-2,42m\cdot (3,3k+1k)=7,594V
Polarização CC com realimentação de tensão
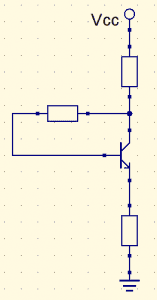
Outra configuração estável, usando a Lei de Kirchhoff das tensões na malha dos terminais base e emissor, pode-se calcular a corrente de base como:
I_{B}=\frac{V_{CC}-V_{BE}}{R_{B}+\beta (R_{C}+R_{E})}
Aplicando a mesma Lei De Kirchhoff na malha coletor-emissor, pode-se obter a tensão coletor-emissor V_{CE}.
V_{CE}=V_{CC}-I_{C}(R_{C}+R_{E})
Um detalhe importante, a corrente que passa por R_{C} não é a corrente do coletor I_{C}. E sim, a que entra no coletor do transistor BJT.
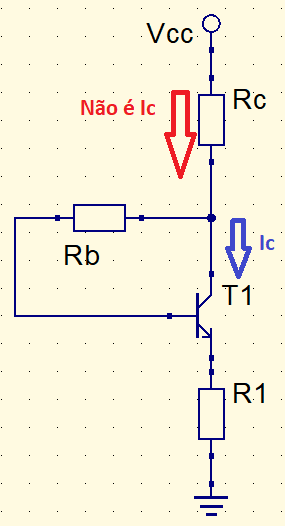
A corrente “Não é Ic” é a soma das correntes da base e do coletor. No entanto, a corrente de coletor e a que passa pelo resistor R_{C} são muito maiores do que I_{B}. As equações mostradas anteriormente foram demonstradas considerando estas correntes como aproximadamente iguais. Com esta aproximação, a corrente de saturação I_{Csat} pode ser calculada como:
I_{Csat}=I_{Cmax}=\frac{V_{CC}}{R_{C}+R_{E}}
Outras configurações de polarizações com transistor BJT
As polarizações com BJT são: base, emissor e coletor comum. Os circuitos mostrados até agora são emissor comum, pois a entrada do circuito é ligada à base e a saída ao coletor.
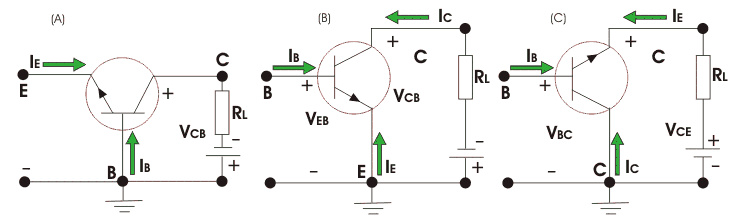
Problemas envolvendo outras configurações podem ser resolvidos aplicando a Lei de Kirchhoff das tensões.
Exemplo de base comum
Considerando este circuito de base comum.
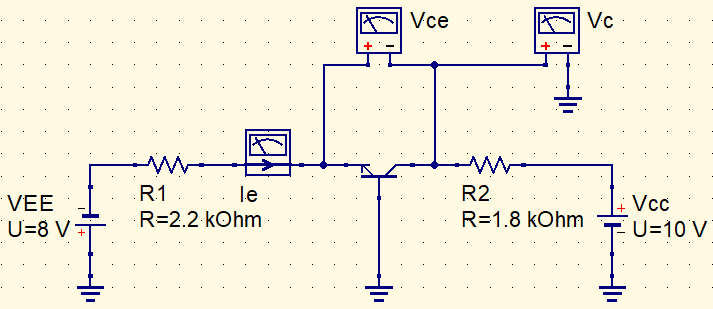
Aplicando a Lei das tensões de Kirchhoff na malha da esquerda.
-V_{EE}+R1\cdot I_{E}+V_{BE}=0
I_{E}=\frac{V_{EE}-V_{BE}}{R_{1}}
I_{E}=\frac{8-0,7}{2,2k}=3,32mA
Calculando V_{C} e considerando a corrente de emissor aproximadamente igual a de coletor (I_{C}\cong I_{E}).
V_{CC}=R2\cdot I_{C}+V_{CB}
10=1,8k\cdot 3,32m+V_{CB}
Como a tensão na base é zero.
V_{CB}=V_{C}=4,024V
E finalmente, encontrando o valor de V_{CE}.
V_{E}-V_{EE}=R_{1}\cdot I_{E}
V_{E}-(-8)=2,2k\cdot 3,32m
V_{E}=-8+7,304=-0,696V
V_{CE}=4,024-(-0,696)=4,72V
Exemplo de coletor comum
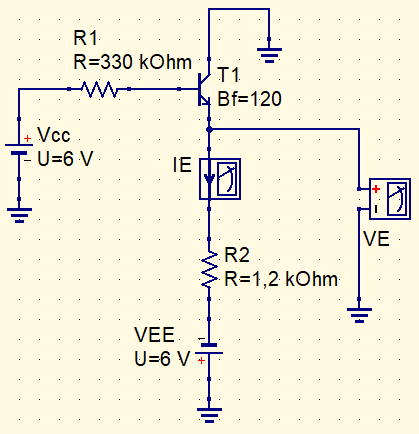
Aplicando novamente a lei de Kirchhoff das tensões.
V_{CC}=I_{B}R1+V_{BE}+I_{E}R2-V_{EE}
V_{CC}+V_{EE}-V_{BE}=I_{B}R1+I_{E}R2
V_{CC}+V_{EE}-V_{BE}=I_{B}R1+I_{B}(\beta +1)R2
I_{B}=\frac{V_{CC}+V_{EE}-V_{BE}}{R1+(\beta +1)R2}
I_{B}=\frac{6+6-0,7}{330k+(120 +1)1,2k}=0,02377m=23,77\mu A
I_{E}=(\beta +1)I_{B}=(120+1)\cdot 23,77\mu =2,88mA
V_{E}-V_{EE}=I_{E}R2
V_{E}-(-6)=2,88m\cdot 1,2k
V_{E}=-2,544V
Base comum com transistor pnp

V_{EE}-V_{BE}=Re\cdot Ie
8-0,7=3,3k\cdot Ie
Ie=2,21mA
Encontrando Vc.
Vc-Vcc=Ic\cdot Rc
Vc-(-12)=2,21m\cdot 3,9k
Vc=-3,37V


