O cíclotron é um acelerador de partículas inventado em 1932, para pesquisas de física de altas energias e produção de isótopos.
Princípio de funcionamento do cíclotron
Foi construído pelo físico americano Ernest Lawrence, junto com seu estudante M. Stanley Livingston. Consiste em dois meio cilindros condutores ocos em forma de “D”, ligados a uma fonte de tensão alternada com alta frequência. Os condutores ficam em uma câmara de vácuo e recebem uma densidade de fluxo magnético uniforme (\vec{B}) e perpendicular.
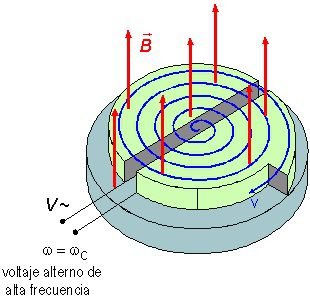
O cíclotron precisa de uma fonte de íons, que fica acima ou abaixo dos condutores em ‘D’. Esta fonte é um gás ionizado por alta tensão, conhecido como plasma, ou um sólido ionizado por um arco voltaico. Os íons são lançados para o centro do cíclotron, entre os condutores e, acelerados por campos elétrico e magnético. Entre os ‘Ds’, há um campo elétrico com intensidade \vec{E}, que exerce uma força elétrica (\vec{F}) sobre a partícula de carga q, a equação desta força é:
\vec{F}=q\cdot\vec{E}
Devido à esta força, a partícula de massa m recebe uma aceleração \vec{a} e ganha velocidade. Usando a Segunda Lei de Newton.
\vec{F}=q\cdot\vec{E}=m\cdot\vec{a}
\vec{a}=\frac{q\cdot\vec{E}}{m}
A diferença de potencial (\Delta V) de um campo elétrico uniforme (\vec{E}) é:
\Delta V=\vec{E}\cdot d
Onde d é a distância entre os condutores. Portanto, a aceleração da partícula no cíclotron é:
\vec{a}=\frac{q\Delta V}{md}
A equação mostra que quanto maior a diferença de potencial, ou tensão, entre os ‘Ds’ e menor a distância entre eles, maior será a aceleração da partícula. Quando a partícula entra na cavidade dos condutores, esta entra em uma região com um campo magnético perpendicular ao campo elétrico, consequentemente, a partícula recebe uma força perpendicular ao vetor velocidade, chamada de Força de Lorentz.
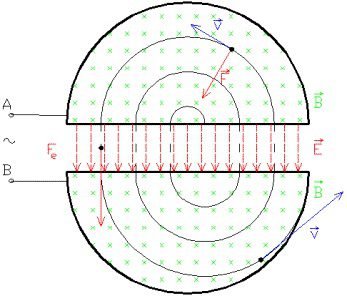
Força de Lorentz
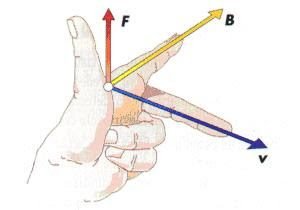
Se a carga for negativa, basta inverter o sentido da força. A equação da força de Lorentz (\vec{F}) é:
\vec{F}=q\vec{v}\times\vec{B}
Onde,
- \vec{v} é o vetor velocidade da partícula.
O \times não é a mesma multiplicação conhecida por todos. Este símbolo é o produto vetorial, usado entre vetores. No caso do cíclotron, a equação da força de Lorentz pode ser simplificada desta forma.
F=qvBsen90^{\circ}
A segunda Lei de Newton aplicada ao movimento circular uniforme.
F=m\frac{v^{2}}{R}
Igualando as duas forças.
qvB=m\frac{v^{2}}{R}
R=\frac{mv}{qB}
Quando a partícula fica entre os ‘Ds’, esta é acelerada pelo campo elétrico, ganhando mais velocidade. Conforme mostra a equação acima, quanto maior a velocidade, maior o raio da trajetória. Por isso que a partícula faz voltas cada vez maiores dentro do cíclotron, até obter velocidade suficientemente alta para sair da região dos ‘Ds’ e atingir um alvo.
Frequência de ressonância
Considerando a velocidade angular (\omega).
\omega=\frac{v}{R}
qvB=m\frac{v^{2}}{R}
v=\frac{qBR}{m}
\omega=\frac{qB}{m}
Com a velocidade angular da partícula, pode-se calcular a frequência de ressonância (f) do cíclotron.
f=\frac{\omega}{2\pi}=\frac{qB}{2\pi m}
O oscilador que alimenta os condutores em ‘D’ deve operar na mesma frequência da frequência de ressonância. Para que a partícula receba uma força elétrica logo que entrar na região do campo elétrico entre os condutores. Quando a partícula alcança velocidades próximas a da luz, a mudança da massa do corpo deve ser considerada.
m=\frac{m_{o}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}
m_{o} é a massa original, c é a velocidade da luz no vácuo e m é a massa do corpo quando atinge velocidades próximas da luz. Portanto, a frequência de ressonância se torna.f=\frac{qB}{2\pi m_{o}}\sqrt{1-\frac{v^{2}}{c^{2}}}
Aplicações atuais do cíclotron
- Produzir isótopos para usar em um aparelho de Tomografia de Emissão de Pósitrons (PET).
- Produção de isótopos para sintetizar radiofármacos para o tratamento de câncer.

- Os cíclotrons ainda são usados em experimentos de física nuclear, para transmutar núcleos atômicos ou bombardeá-los.


