Teoremas booleanos

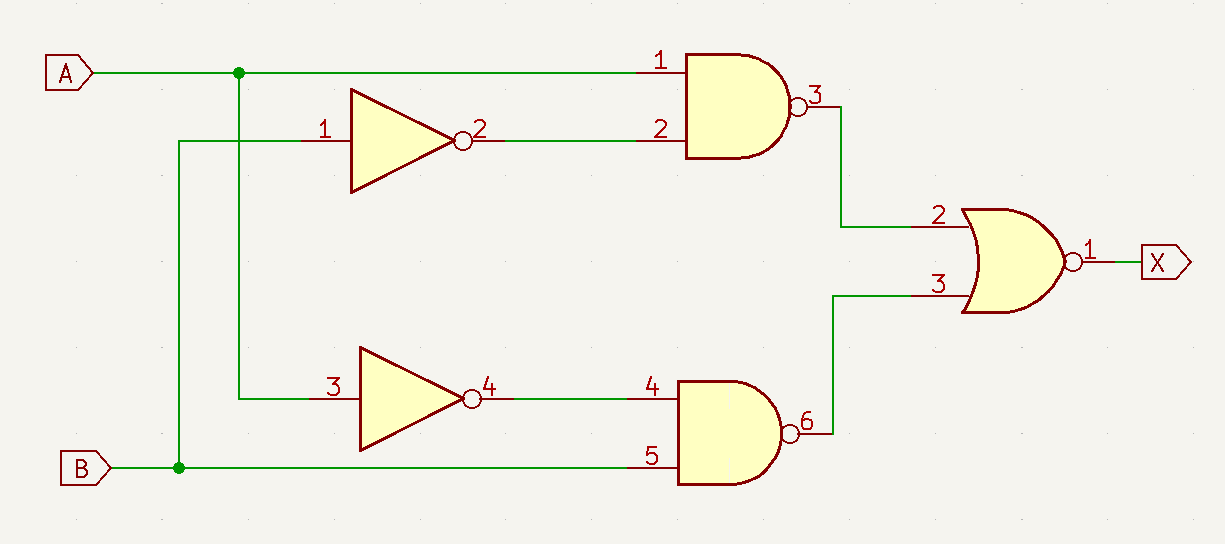
Os teoremas booleanos são um conjunto de regras da álgebra booleana para simplificar as expressões lógicas dos circuitos combinacionais.

Post sobre circuitos combinacionaisClique aqui

A álgebra booleana é uma ferramenta matemática fundamental para a computação digital, onde as variáveis e as funções têm apenas valores binários de “0” ou “1”. Foi introduzida em 1854 pelo matemático britânico George Boole. Nesta álgebra, o sinal de adição (+) representa a operação lógica OU e o sinal de multiplicação (\times ou \cdot) representa a operação lógica E.

Teoremas booleanos com uma variável

Toda variável é representada por uma letra, a negação desta variável geralmente é representada por um traço encima da letra. Por exemplo, \overline{A} é a negação de A, portanto, \overline{A} sempre terá o valor binário inverso de A. Eis a lista de teoremas com apenas uma variável.

• A+0=A

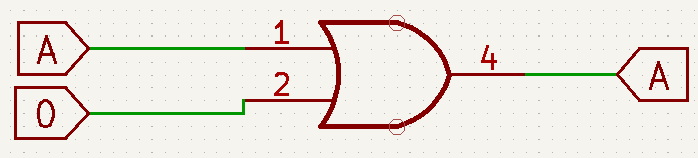
• A+1=1

• A+A=A

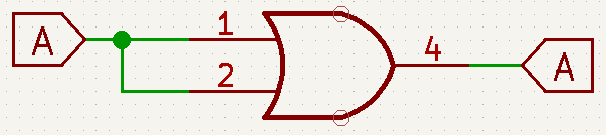
• A+\overline{A}=1

• A\cdot 0=0

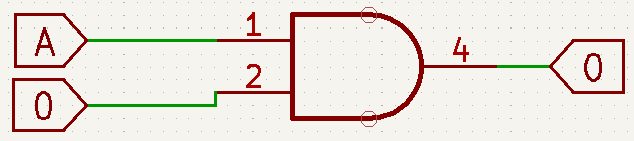
• A\cdot 1=A

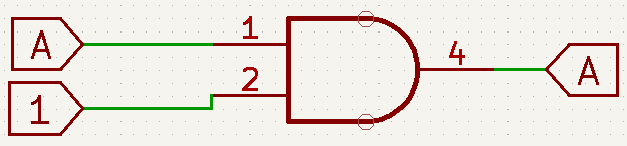
• A\cdot A=A

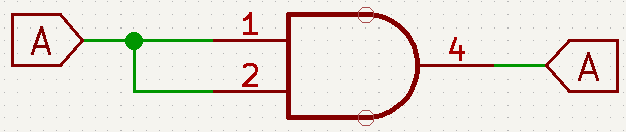
• A\cdot\overline{A}=0

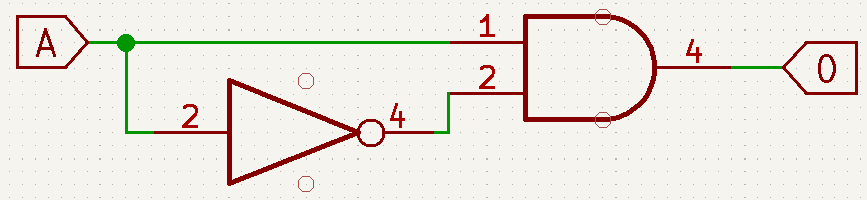
Teoremas booleanos com duas ou três variáveis

• A+B=B+A
• A\cdot B=B\cdot A
• A+(B+C)=(A+B)+C=A+B+C
• A(BC)=(AB)C=ABC
• A(B+C)=AB+AC
• (A+B)(C+D)=AC+AD+BC+BD
• A+AB=A
• A+\overline{A}B=A+B
• \overline{A}+AB=\overline{A}+B

Teoremas de De Morgan

Estes são muito úteis na manipulação de expressões lógicas.

\overline{(A+B)}=\overline{A}\cdot \overline{B}

\overline{(A\cdot B)}=\overline{A}+\overline{B}

Comprovando os teoremas de De Morgan com uma tabela verdade e considerando todas as possibilidades.

\overline{(A+B)}=\overline{A}\cdot \overline{B}

\overline{(A\cdot B)}=\overline{A}+\overline{B}

Para que servem os teoremas booleanos?

Com estes teoremas, os circuitos combinacionais podem ser simplificados para que tenham apenas um tipo de porta lógica como a NAND ou a NOR, visto que os circuitos integrados comerciais de portas lógicas usam apenas um tipo de porta.