Este método gráfico simplifica uma equação lógica de um circuito combinacional. Para entender circuitos combinacionais clique neste botão:
Circuitos Combinacionaisclique aqui
Este método é útil quando o circuito possui 4, 5 ou 6 entradas de variáveis.
Procedimento
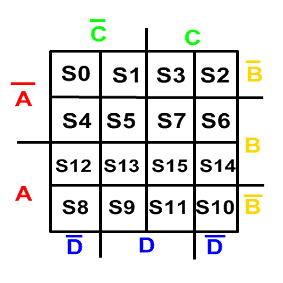
Aqui está um exemplo com 4 variáveis, primeiro monta a tabela verdade:
Depois constrói-se o mapa de Karnaugh e coloca o “1” onde a combinação de entrada der sinal alto na saída, nos demais põe-se o “0”.
Olhando para o mapa, pode-se simplificar o circuito combinacional da seguinte forma:
A equação lógica fica:
X=AB+\bar{C}D
E se o mapa ficasse desta forma:
Poderia simplificar da seguinte forma:
E ficaria assim:
X=B
Outras formas possíveis de combinação, dependendo do mapa:
X=\bar{B}\bar{D}
X=A\bar{D}
X=\bar{B}
X=\bar{C}D+BC\bar{D}+\bar{A}\bar{B}CD
O segredo é pegar o maior número de “uns” possíveis com o menor número possível contornos.
5 ou 6 variáveis
Para usar o mapa com 5 variáveis, deve-se fazer dois mapas de 4, um com A=0 e outro com A=1 e resolver ambos.
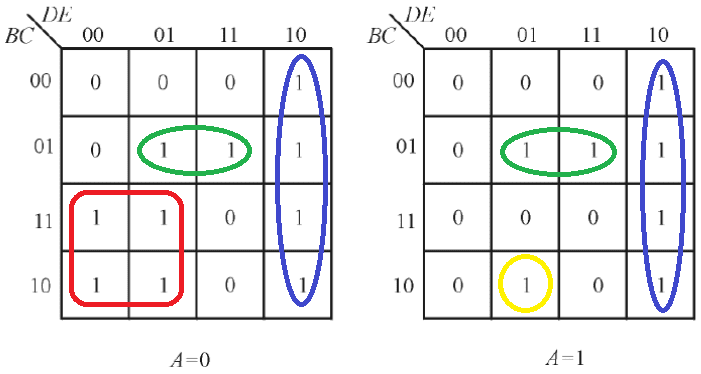
Os contornos que estão apenas no mapa A=0 terão \bar{A} na expressão, enquanto que os contornos que estão apenas no mapa A=1 terão A na expressão. Portanto, a equação ficará assim:
Para 6 variáveis é a mesma coisa, porem com 4 mapas.
