Atendendo a pedidos, o assunto é sobre conceitos básicos de CA. Já foi mencionado CA no post sobre eletromagnetismo, este post entrará mais a fundo.
Para ver conceitos básicos de eletromagnetismo, clique no botão abaixo.
Propriedades da onda
O que é frequência? É o número de ciclos por segundo em Hertz (Hz), este ciclo pode ser o balançar de um pêndulo, a mudança de intensidade e sentido de uma corrente elétrica, o número de voltas que um objeto percorre em trajetória circular, a variação de amplitude de uma onda sonora, etc.
1 Hz = 1 ciclo por segundo
O período T simplesmente é o tempo necessário para completar um ciclo e o inverso da frequência f.
T=\frac{1}{f}
Toda onda tem amplitude, que é a distância entre a crista ou vale e o ponto “zero” da onda.

Um comprimento de onda (\lambda) é a distância entre dois picos ou vales.

Esta é a fórmula para calcular o comprimento de uma onda, v é a velocidade.
\lambda=\frac{v}{f}
Esta é a fórmula da velocidade angular em radianos por segundo (rad/s).
\omega =2\pi f
Outras definições
- Valor instantâneo: É o valor da amplitude em um determinado tempo.
- Valor pico-a-pico (V_{p-p}): É a soma das amplitudes positiva e negativa. No exemplo abaixo, a tensão pico-a-pico da onda de amplitude 10 V é 20 V.

- Valor eficaz ou RMS (V_{rms}): É o valor da tensão ou corrente equivalente ao valor CC. Um sinal alternado com valor eficaz de 10 V fornece a mesma potência para uma resistência se fosse um sinal DC de 10 V. O valor eficaz de uma tensão ou corrente é igual a 0,707 do valor máximo V_{m} ou I_{m}.
I_{rms}=\frac{I_{m}}{\sqrt{2}} ou V_{rms}=\frac{V_{m}}{\sqrt{2}}

A demonstração envolve usar uma identidade trigonométrica e igualar a potência média CA com a potência CC.
- Valor médio: É calculado dividindo a área contornada pela curva pelo período. Uma onda que tem áreas positiva e negativa iguais em um período completo tem valor médio zero.

Para calcular o valor médio de um semiciclo de senoide, temos que usar integrais que chegam ao resultado mostrado abaixo.
V_{av}=\frac{2}{\pi }V_{m}=0,637V_{m}
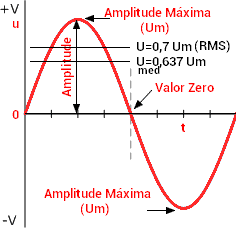
Descrição da onda senoidal CA
Um sinal senoidal CA é representado por esta equação. t é o tempo.
V(t)=V_{m}sen(2\pi ft+\phi )
\phi é o ângulo de fase em graus ou radianos, representa a posição da onda em relação ao tempo inicial. Se a onda começa em t=0, então \phi é igual a zero. Se a onda começa antes de t=0, ela está adiantada e \phi é positivo. Se começa depois de t=0, ela está atrasada e \phi é negativo.

Indutores puros em CA têm a tensão 90° ou \frac{\pi }{2} adiantada em relação à corrente.
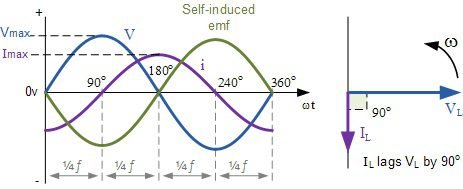
Capacitores puros em CA têm a corrente 90° ou \frac{\pi }{2} adiantada em relação à tensão.

Uma cossenoide é uma curva adiantada 90° em relação à senoide.

O diagrama fasorial é outra forma de representar uma senoide. A curva é representada por um vetor chamado fasor, que gira no sentido anti-horário na velocidade \omega. O ângulo de fase representa o ângulo que o fasor forma em relação ao eixo horizontal.
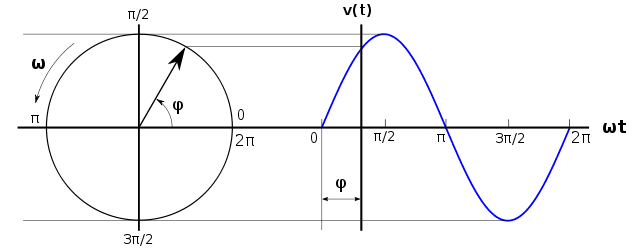
Esta é a forma fasorial de representar uma tensão ou corrente CA.
V=V_{rms}\angle \phi


Legal…estou aprendendo muito…tem alguns livros para indicar sobre esse assunto???
Eu tenho o livro “Introdução à Análise de Circuitos”, 12 edição, cujo autor é Robert L. Boylestad, da editora Pearson.