This is one more post about artificial intelligence. An introduction about bayesian networks and your applications are this post’s subject.
What they are?
Bayesian networks are graphic models which work with uncomplete knowledge and allow machines to make inferences, predictions and take decisions from probability of variables to assume some states. With bayesian networks, machines can make predictions like “If event X happens, there is high probability to happen Y”. Example of variables: “Have any disease?”, “Will event X happen?”, age, height. Examples of states: “true or false”, “full, empty, tank with much or few fuel?”.
How it works?
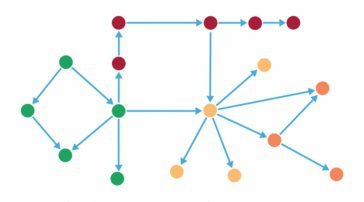
It has nodes and connections, each node represents a variable that can be discrete or continuous, this variable has probabilities to assume some states. A node can have more than one variable and can influence other network’s nodes, which are connected with the node. This is an example of bayesian network working only with discrete variables, when choose arbitrarily the states in some nodes, it will influence the probability in other nodes.
[WPGP gif_id=”8010″ width=”600″]
This is a bayesian network with continuous and discrete variables.

To play with these bayesian networks, click in this link and this one. These types of network use Bayes Theorem to calculate the probability of certain events with some available information.
P(A|B)=\frac{P(B|A)P(A)}{P(B)}
- P(B) and P(A) are the probabilities to occur B and A respectively;
- P(A|B) is the probability to occur A, considering that event B happened, or given B;
- P(B|A) is the probability to occur B given A.
Dynamic bayesian networks
The dynamic bayesian networks include time and events happen in sequence. In this type of network, nodes are divided in time slots.

These networks can be used to model biological systems like cell cycles, gene regulators and central nervous system, because these have variable which change in time.
Other applications
In addition to artificial intelligence (AI), other applications are:
- Disease diagnostic from symptoms;
- Build economic models;
- Simulation games to educational and entertainment ends;

- Calculation and risk management;
- Chemical analysis.