Circuit analysis with op-amp (Part 1)

This is the first part of a series of posts that show an analysis of practical circuits that use an operational amplifier (op-amp).

Post about the working principle of operational amplifier.Click here

In this post, op-amps will be considered as ideals.

Circuits with op-amp

Inverter amplifier

Considering the op-amp circuit below.

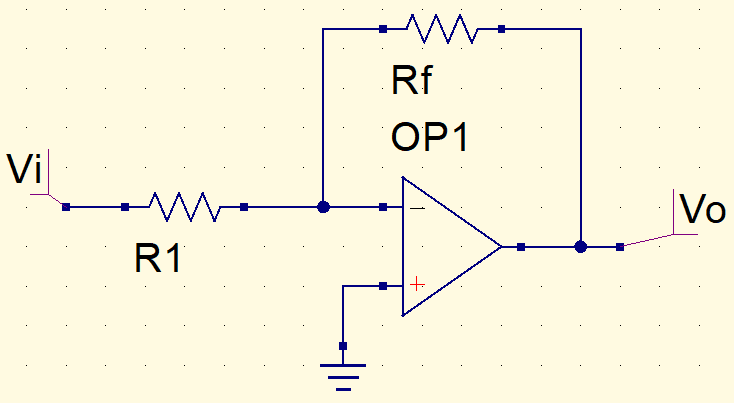
This is the equivalent circuit.

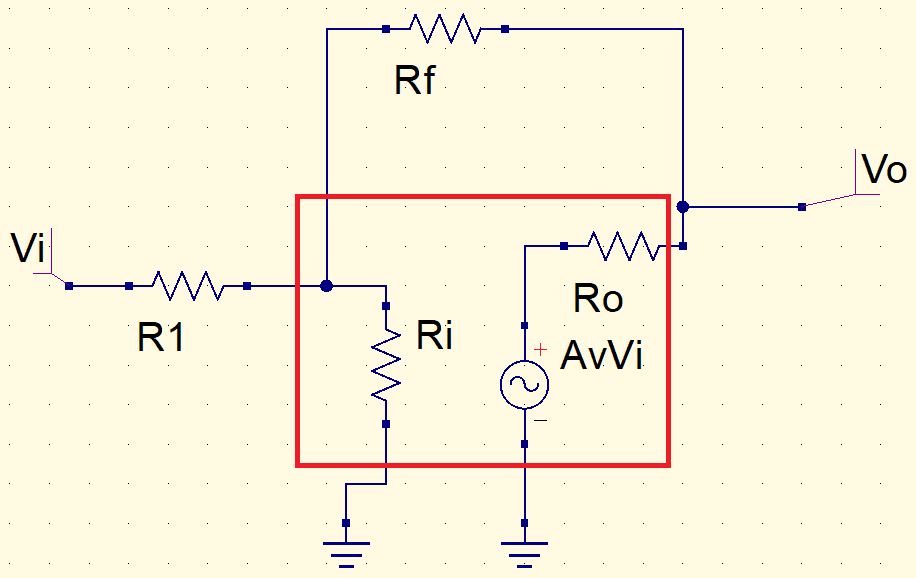
In an ideal op-amp, input impedance is infinite and output impedance is zero. Therefore, the equivalent circuit is,

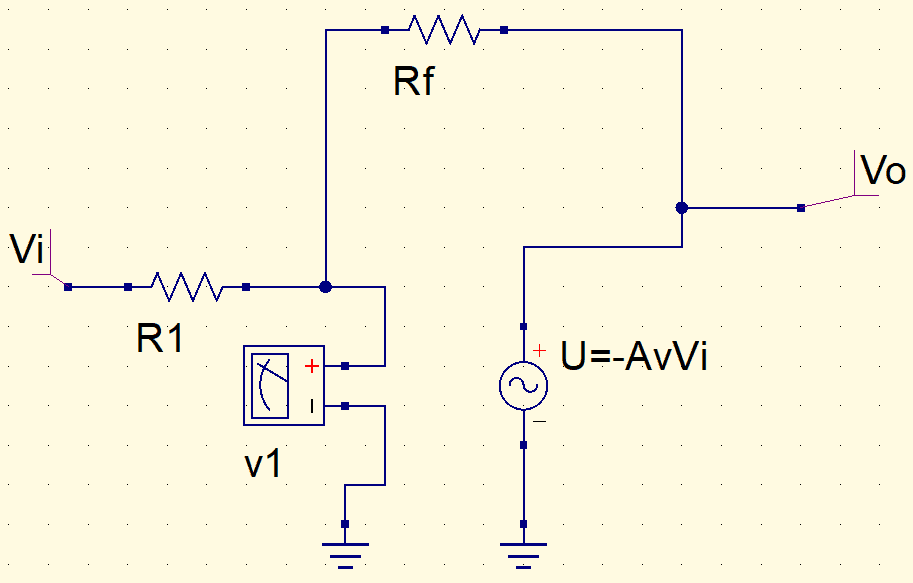
Applying the superposition theorem to find v1 voltage. Considering AvVi as zero.

$v1_{1}=\frac{Rf}{R1+Rf}\cdot Vi$

And Vi as zero.

$v1_{2}=\frac{R1}{R1+Rf}\cdot(-AvVi)$

$v1=v1_{1}+v1_{2}=\frac{Rf}{R1+Rf}\cdot Vi+\frac{R1}{R1+Rf}\cdot(-AvVi)$

$v1=\frac{RfVi}{Rf+(1+Av)R1}$

Usually, $Av$ is much higher than 1 and $AvR1$ is much higher than $Rf$ , therefore the equation becomes,

$v1=\frac{RfVi}{AvR1}$

The relation between output voltage and resistors.

$\frac{Vo}{v1}=\frac{-Av\cdot v1}{v1}=-\frac{-AvRfVi}{v1AvR1}$

This is the inverter amplifier output voltage equation.

$V_{o}=-\frac{R_{f}}{R_{1}}\cdot V_{i}$

Non-inverter amplifier

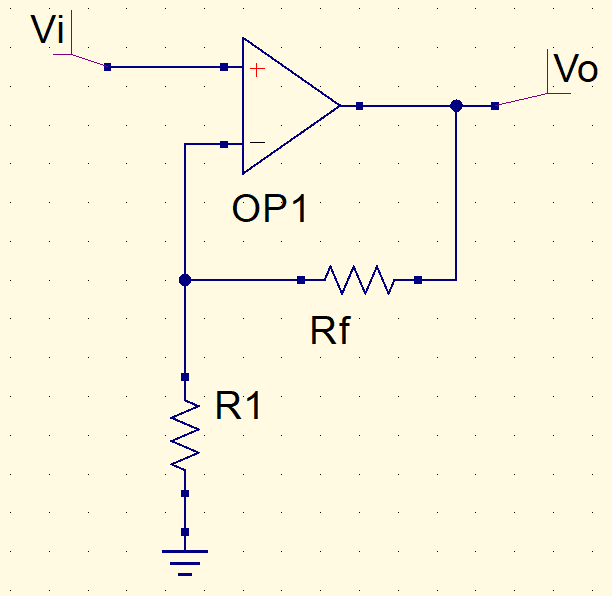
Using the voltage division equation, this result is reached.

$V_{o}=\left (1+\frac{Rf}{R1}\right )\cdot V_{i}$

Voltage buffer

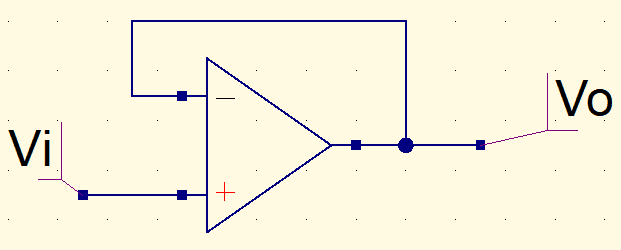
On a voltage buffer or unity amplifier, voltage output is equal to voltage input.

Amplifier adder

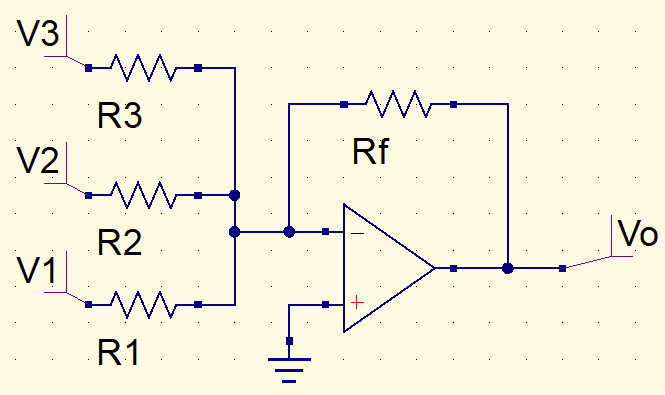
The equation is the sum of many inverters amplifiers.

$V_{o}=-\left(\frac{Rf}{R1}\cdot V1+\frac{Rf}{R2}\cdot V2+\frac{Rf}{R3}\cdot V3\right)$

Consider the circuit example below, which is an adder amplifier with commercial resistors, let’s calculate output voltage Vo.

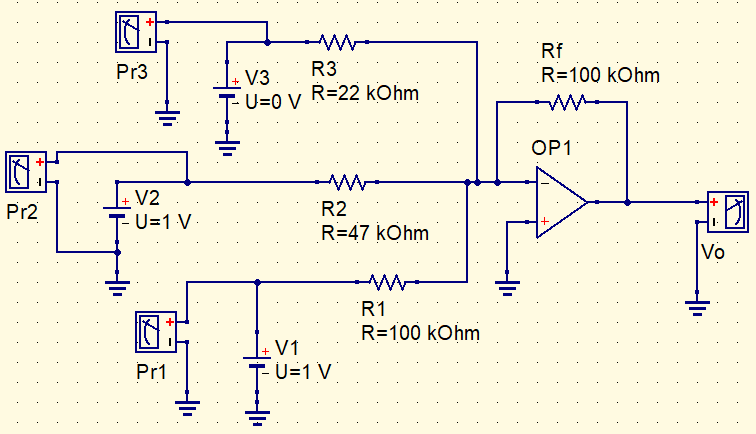
Applying the equation.

$Vo=-\left(\frac{100k}{22k}\cdot 0+\frac{100k}{47k}\cdot 1+\frac{100k}{100k}\cdot 1\right)$

$Vo=-\left(2,12\cdot 1+1\cdot 1\right)=-3,13V$

The result of circuit simulation.

Now, let’s make an adjustment on input voltages.

Applying again the same equation.

$Vo=-\left(4,54\cdot 1+0+1\cdot 1\right)=-5,54V$

And making the simulation.

What this example shows is that the adder can be used as a digital-analog converter (DAC). Input with R3 resistor is the most significative bit (MSB) and input with R1 is the least significative bit (LSB). In the first simulation, inputs were ‘011’, which generated close to 3V, since ‘011’ is 3 in binary. While on the second simulation, inputs were ‘101’, which is 5 in binary, and output was close to five.

Integrator

On inverter, if the feedback resistor is replaced by a capacitor, the circuit becomes an integrator. Considering virtual ground.

$I=\frac{Vi}{R}=-\frac{Vo}{X_{C}}$

X_{C}

is capacitive reactance.

$X_{C}=\frac{1}{j\omega C}=\frac{1}{sC}$

On Laplace notation, $j\omega=s$ .

$\frac{Vi}{R}=-\frac{Vo}{\frac{1}{sC}}=-sCVo$

$\frac{Vo}{Vi}=\frac{-1}{sCR}$

Putting the equation on time domain.

$v_{o}(t)=-\frac{1}{RC}\int v_{i}(t)dt$

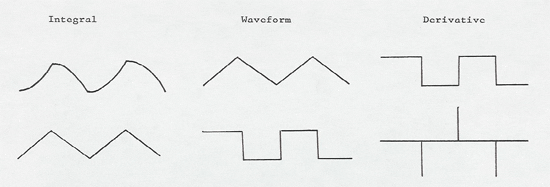
If the integrator’s input is a square wave, output will be a triangular wave. If input is a triangular wave, the output will be like the wave on top left. The square wave is the integral of pulse wave, shown on bottom right. Source: UCLA.

In input is a sine wave, output will be a sinusoid delayed 90º in relation to input.

Differentiator

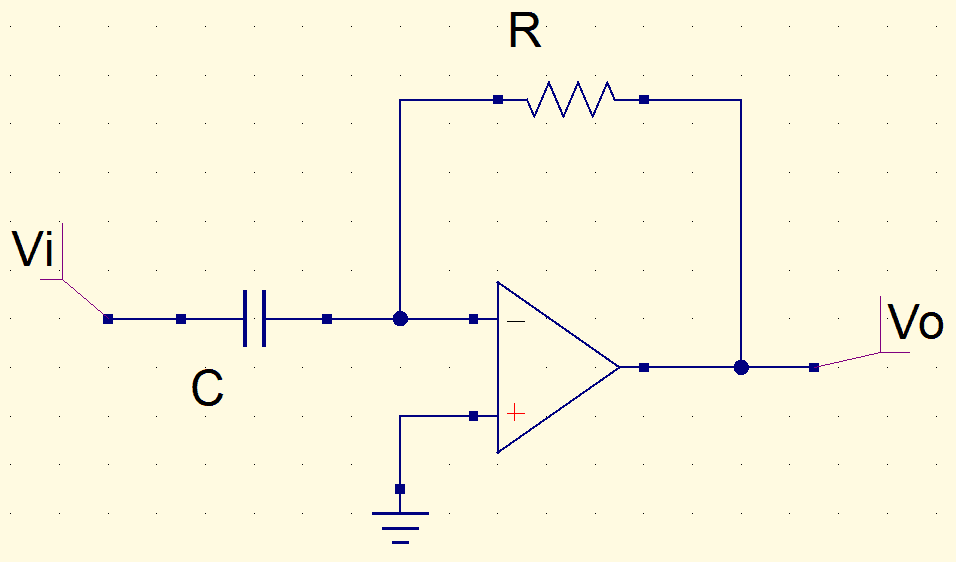
By switching positions of resistor and capacitor, we have the differentiator, which is the opposite of the integrator. Therefore, output signal is derivative of input signal. In this circuit, if the input is a sinusoid, the output will also be a sinusoid, but 90º early in relation to input. Below is the equation of output voltage on time domain.

$v_{o}(t)=-RC\frac{dv_{i}(t)}{dt}$