Efeito pelicular: o que é?

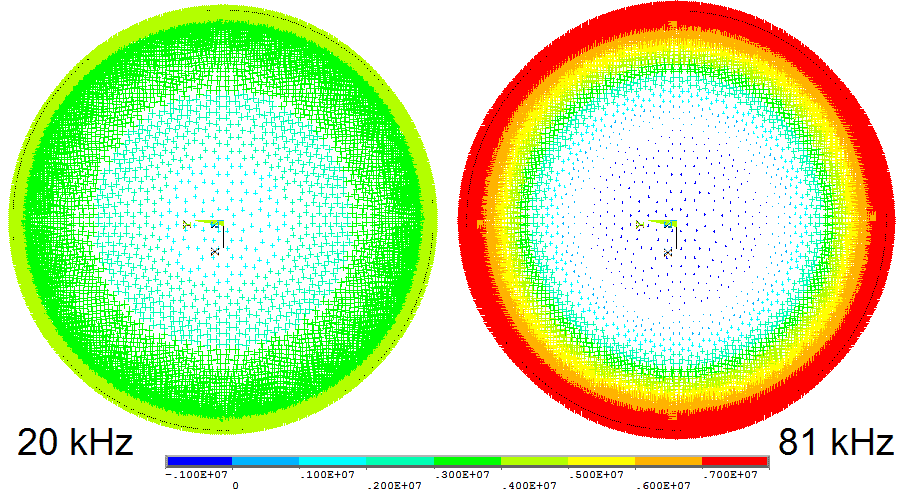
O efeito pelicular aparece em linhas de transmissão que transportam corrente alternada. A causa deste efeito é explicada neste post.

O fenômeno

Em corrente contínua, os elétrons se distribuem e se movem uniformemente em uma seção do condutor. Porém, com uma corrente alternada, um campo magnético variável é produzido devido à constante mudança de sentido das cargas elétricas.

No centro, as correntes $I$ e $I_{W}$ possuem sentidos opostos e se cancelam. Enquanto na periferia, estas correntes se somam. O resultado é o aumento da densidade de corrente na periferia do fio e a redução próxima do centro. Quanto maior a frequência, maior o efeito pelicular.

Por isto que não se deve usar fios maciços para transmitir sinais CA de alta frequência. Nestas situações, são usados condutores ocos, economizando peso e custo com materiais.

Resistência CA

Por causa do efeito pelicular, devem ser considerados dois tipos de resistências: CC e CA. A relação entre as resistências é dada pela equação.

$R_{CA}=R_{CC}\cdot k\sqrt{f}$

• $R_{CA}$ e $R_{CC}$ são as resistências CA e CC respectivamente.
• $f$ é a frequência em Hertz (Hz).
• O fator $k$ depende do diâmetro do fio na escala americana AWG.

Profundidade de penetração do efeito pelicular

Quando aumenta a frequência da corrente, a densidade de corrente no interior do condutor cai exponencialmente e se concentra nas bordas do fio. A profundidade de penetração vai da superfície, até onde há somente 37% da densidade de corrente na superfície.

A equação da densidade de corrente $J$ em uma profundidade.  

$J=J_{s}e^{\frac{-d}{\delta }}$

• $J_{s}$ é a densidade de corrente na superfície.
• $d$ é o diâmetro do condutor.
• $\delta$ é a profundidade onde há densidade de corrente, fica menor quando aumenta a frequência.

Para calcular $\delta$.

$\delta =\sqrt{\frac{2\rho }{\omega \mu }}$

• $\rho$ é a resistividade elétrica do condutor em $\Omega \cdot m$.
• $\omega$ é a frequência ângular em radianos por segundo, pode ser calculado da seguinte forma.

$\omega =2\pi f$

• $\mu$ é a permeabilidade magnética em H/m, que é o produto da permeabilidade relativa do material $\mu _{r}$ e da permeabilidade magnética no vácuo $\mu _{o}$, cujo valor é $1,26\cdot 10^{-6} H/m$.

$\mu =\mu _{r}\mu _{o}$

Com manipulações, a profundidade de penetração também pode ser expressa da seguinte forma.

$\delta =\sqrt{\frac{1}{\pi f\sigma \mu_{r}\mu _{o}}}$

• $\sigma$ é a condutância, o inverso da resistividade.